Реферат: Модернизация АСР (автоматическая система регулирования) молотковой дробилки типа ДДМ

,а в левой - выходная величина и ее производная.

Р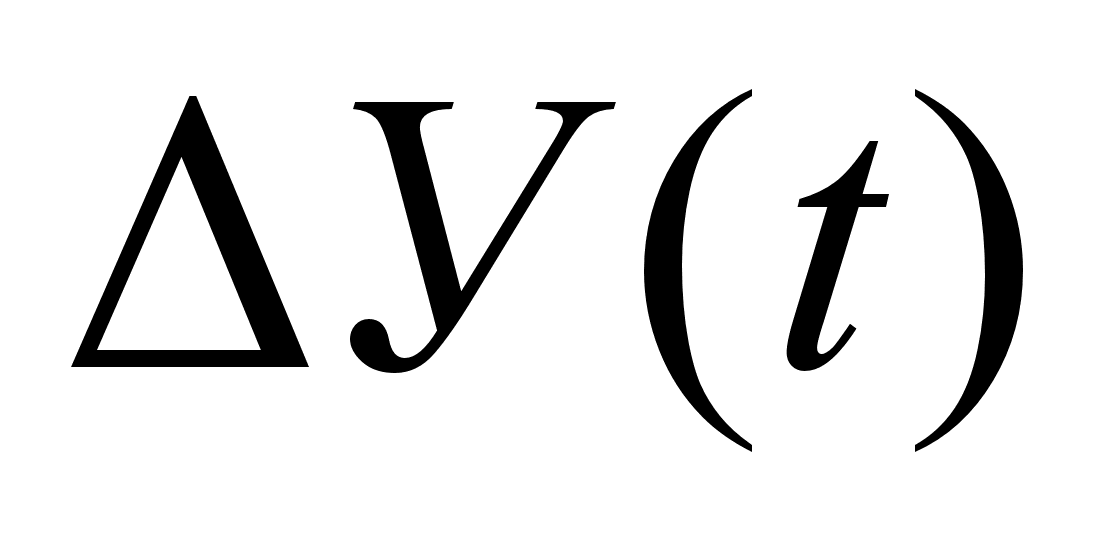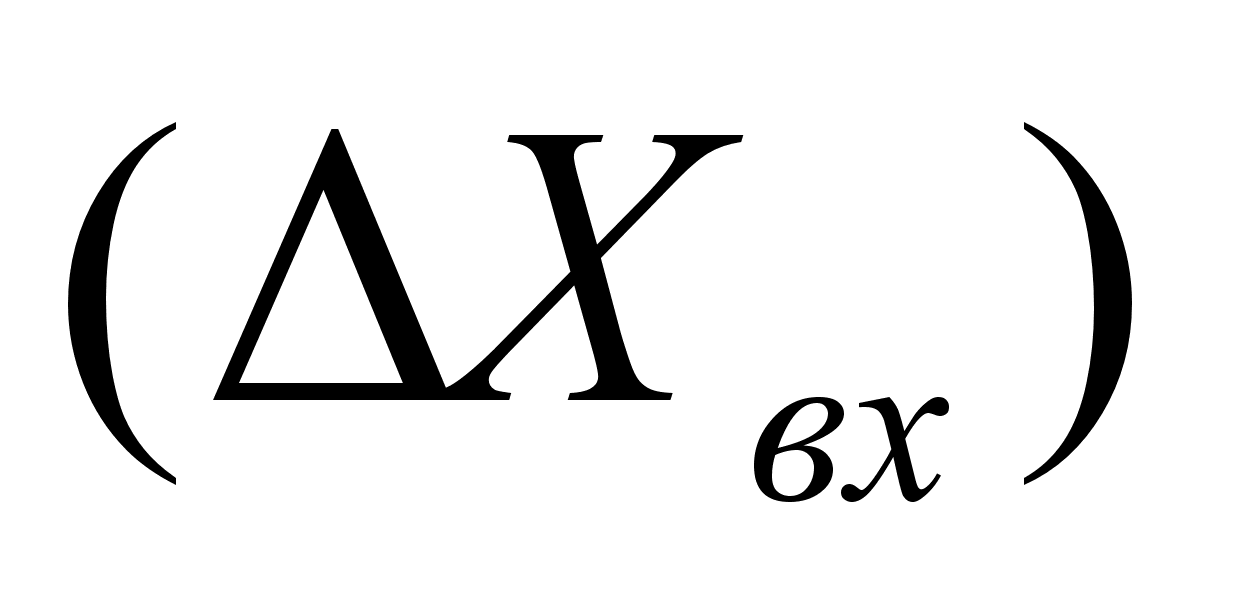ешением уравнения (1.1) есть уравнение функции

по которой можно построить переходную характеристику ОУ при известном значении входного действия .

В результате исследования реального ОУ для вычисления его динамических параметров необходимо провести цикл экспериментов для вычисления Т1,

Т2, Ко.

В случае, когда эти параметры известны или заданы, по ним можно смоделировать переходной процесс.

Для этого выполняем следующие действия:

1. З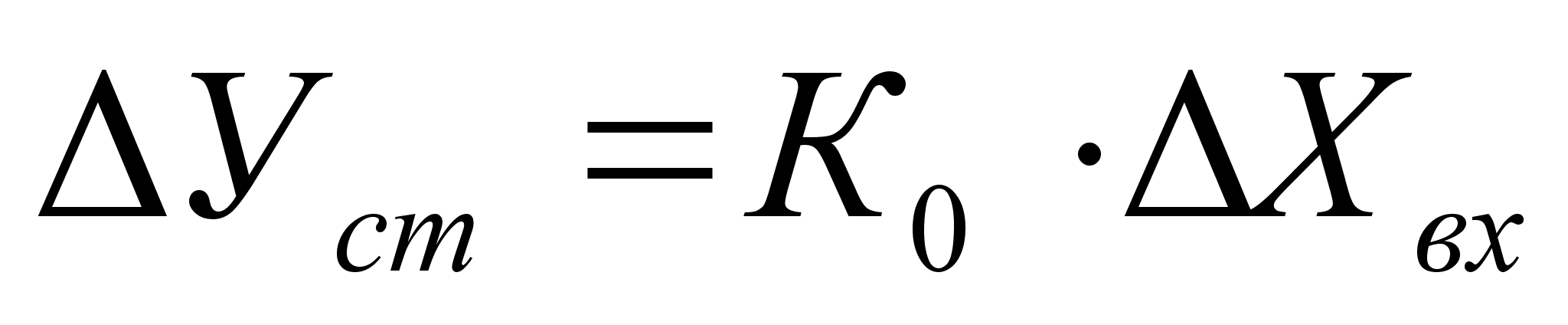аписываем уравнение статики

которое получаем из уравнения (1.1).

2) Чтобы рассчитать переходной процесс в динамике необходимо решить уравнение 1.1. Его решение при нулевых начальных условиях имеет вид:

где e --- основа натурального логарифма

t --- время

С помощью уравнения (1.2) можно рассчитать переходную характеристику объекта. Вычисляем приблизительную длительность процесса по формуле:

tп ≈ 3(Т1+Т2) (1.3)

Время tп разделим на 20 – 25 одинаковых интервалов. Подставим свои значения в формулу 1.3.

tп ≈ 3(35+70) = 315;

Тогда интервал равен t ≈ 315:25=12,6 мин.

Примем интервал = 13.

Теперь подставим в уравнение (1.2) значение времени (t) кратные выбранному интервалу, найдём значение выходной величины в выборе момента времени.

Результат подсчетов запишем в виде таблицы.

Таблица 1.1

Время tмин (с)	Регулируемая величина ∆У,С
0,0	0,00
20,0	0,00
33,0	0,57
46,0	1,93
59,0	3,65
72,0	5,50
85,0	7,32
98,0	9,03
111,0	10,58
124,0	11,97
137,0	13,19
150,0	14,24
163,0	15,15
176,0	15,92
189,0	16,58
202,0	17,14
215,0	17,61
228,0	18,00
241,0	18,33
254,0	18,61

Необходимо иметь в виду, что из-за появления транспортного запаздывания, все значения ДУ будут сдвинуты на величину Т. По найденным значениям на мелиметровке строим график.

2.АППРОКСИМАЦИЯ ПЕРЕХОДНОЙ ХАРАКТЕРИСТИКИ.

При анализе свойств элементов АСР в основном используют аппроксимированные характеристики для упрощения процесса анализа и уменьшения количества расчетов.

Так элемент, что является апериодическим типовым звеном второго порядка можно аппроксимировать, как апериодическое звено первого порядка последовательно соединенного с запаздывающим звеном.

Таким образом, мой ОУ может быть представлен как аналогичное соединение с такой разницей, что запаздывающее звено будет иметь как чистое транспортное запаздывание, так и емкостное за счет инерционности апериодического звена. Соединение имеет вид: Рисунок 2.1