Реферат: Некоторые Теоремы Штурма

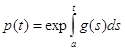(1.4)

при некотором a€J. Частичное обращение этого утверждения также верно, поскольку если функция р(t) непрерывно дифференци­руема, уравнение (1.2) можно записать в виде

,

а это уравнение имеет вид (1.1).

В случае, если функция р (t) непрерывна, но не имеет непрерыв­ной производной, уравнение (1.2) не может быть записано в виде (1.1). Тогда уравнение (1.2) можно интерпретировать как линейную систему из двух уравнений первого порядка для неизвестного двумерного вектора :

, . (1.5)

Другими словами, решение и = и (t) уравнения (1.2) должно быть такой непрерывно дифференцируемой функцией, что функция р(t) u'(t) имеет непрерывную производную, удовлетворяющую (1.2). Если р(t) ¹ 0 и q(t), h(t) непрерывны, к системе (1.5), а потому и к уравнению (1.2) применимы стандартные теоремы существования и единственности для линейных систем (Мы можем рассматривать также более общие (т. е. менее гладкие) типы решений, если предполагать, например, только, что функции 1/p(t), q (t), h (t) локально интегрируемы.)

Частному случаю уравнения (1.2) при соответствует уравнение

и" + q(t) u = h(t). (1.6)

Если функция принимает вещественные значения, урав­нение (1.2) может быть приведено к такому виду с помощью замены независимых переменных

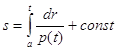, т.е. (1.7)

при некотором a € J. Функция s = s (t) имеет производную и потому строго монотонна. Следовательно, функция s = s (t) имеет обратную t= t (s), определенную на некотором s-интервале. После введения новой независимой переменной s урав­нение (1.2) переходит в уравнение

(1.8)

где аргумент t выражений p(f)q(t) и p(t) h(f) должен быть заме­нен функцией t = t(s). Уравнение (1.8) является уравнением типа (1.6).

Если функция g (t) имеет непрерывную производную, то урав­нение (1.1) может быть приведено к виду (1.6) с помощью замены неизвестной функции и на z :

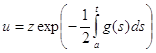(1.9)

при некотором a € J. В самом деле, подстановка (1.9) в (1.1) приводит к уравнению

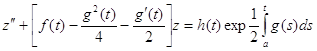(1.10)

которое имеет вид (1.6).

В силу сказанного выше, мы можем считать, что рассмат­риваемые уравнения второго порядка в общем случае имеют вид (1.2) или (1.6). Утверждения, содержащиеся в следующих упраж­нениях, будут часто использоваться в дальнейшем.

§ 2. Основные факты

Прежде чем перейти к рассмотрению специальных вопросов, мы получим следствия, касающиеся однородного и неоднородного уравнений

(2.1)

(2.2)

Для этого перепишем скалярные уравнения (2.1) или (2.2) в виде системы двух уравнений

(2.3)

(2.4)

где векторы х= (х¹ , х² ), у == (у¹ , y² ) совпадают с векторами , , A(t)- матрица второго порядка:

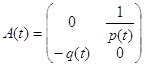(2.5)