Реферат: Некоторые Теоремы Штурма

Если замкнутый ограниченный интервал [a,b] содержится в J, то, полагая

, ,

мы получаем из (2.14) частное решение

.(2.15)

Оно может быть записано в виде

, (2.16)

где

(2.17)

матрица С (t) зависит от , но не зависит от их про­изводных. В этом случае уравнение (2.1) и эквивалентная ему система (2.3) сводятся к системе

. (2.28)

(xii) Если известно частное решение уравнения (2.27), не равное нулю на J, то мы можем определить линейно независимые решения с помощью квадратур (см. (ix)) и затем найти матрицу, вхо­дящую в (2.28). В действительности, тот же результат можно полу­чить более прямым путем. Пусть уравнение (2.27) имеет решение на интервале J . Заменим неизвестную функцию и в (2.1) на z , так что

. (2.29)

Функция z удовлетворяет дифференциальному уравнению

.

Умножая его на , мы получаем, что

(2.30)

или, в силу (2.27), что

, (2.31)

т. е. подстановка (2.29) приводит уравнение (2.1) к (2.30) или к (2.31). Мы могли также начинать не с решения дифферен­циального уравнения (2.27), а с функции , имеющей непрерывную производную и такой, что непрерыв­но дифференцируема. При этом определяется равенством (2.27), так что . Подстановка (2.29) будет назы­ваться также вариацией постоянных.

(xiii) Подстановка Лиувилля. В качестве частного случая рас­смотрим (2.1) с р (t) = 1:

и" + q (t) и = 0. (2.32)

Предположим, что функция q (t) имеет непрерывную производную второго порядка, вещественна и не равна нулю, так что

±q (t) > 0, где ± = sgn q (t) (2.33)

не зависит от t. Рассмотрим вариацию постоянных

. (2.34)

Тогда (2.32) сводится к (2.30), где , т. е. к уравнению

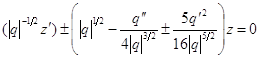(2.35)

Замена независимых переменных , определенная соотношением

, (2.36)