Реферат: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам

2. Творчески изучая и классифицируя их, найти обобщение и решение этих задач для конкретных многосвязных областей (см. оглавление).

Данная работа состоит из введения и 6 параграфов.

В введении обосновывается постановка задачи, показывается актуальность рассматриваемой темы дипломной работы, дается краткий анализ и перечень работ по данному исследованию (1 – 24).

Параграфы (§1, §2) не только вспомогательные материалы, необходимые для понимания основного содержания дипломной темы, но и являются справочной классификацией о задачах Дирихле (классическая, обобщенная, общая, видоизмененная) для любой связности заданной области G = G (w ) и задачах Шварца-Пуассона (для круга, кругового кольца, внешности кругов, для полуплоскости).

В §3 интегральная формула Анри Вилля – проблема Дирихле для кругового кольца в форме Ахиезера преобразована и получена новая компактная, контурная, структурная формула А.Вилля для кругового кольца. Здесь же, ввиду важности трех функций I (u ), (u ) и (u ) для практического приложения и простоты реализации на ЭВМ, мы рассмотрели все варианты представления рядов данных функций (37) – (48) по справочникам [19] – [22] специальных функций (а), б)).

Параграфы §4 - §6 – основное содержание самостоятельной работы автора: рассмотрены применение теории комфорного отображения к краевым задачам – решение задачи Дирихле методом Чизотти для заданных областей (§4).

В §5 – интегральные представления Пуассона-Дирихле для круга, кругового кольца и, наконец, §6 – интегральная формула Чизотти-Шварца-Пуассона-Дирихле для конечных трехсвязных областей.

Оглавление – ясное представление о единстве всех классических задач и о содержании предлагаемой работы (см. оглавление!).

В данной работе все найденные решения выписываются почти в явном виде и параметры, фигурирующие в постановке задачи, определяются явно и однозначно.

Основное содержание дипломной работы являются некоторыми обобщениями курсовых работ и самостоятельной работы автора.

§1. О задачах Дирихле.

а) Задача Дирихле для круга – Задача Пуассона

(классическая формулировка).

1. Задача нахождения функции, гармонической в некоторой области была названа Риманом задачей Дирихле. В классическом виде эта задача формулируется следующим образом.

Пусть на границе области D ⁺ задана непрерывная функция f (). Найти непрерывную в и гармоническую внутри области D ⁺ функцию U (z ), принимающую на границе значения f (). Таким образом, требуется, чтобы U (z ) стремилась к f (), когда z D ⁺ стремится к , u (z ) → f (), при z → .

Задача Дирихле представляет интерес для физики. Так, потенциал установившегося движения несжимаемой жидкости, температура, электромагнитные и магнитные потенциалы – все являются гармоничными функциями.

Примером физической задачи, приводящей к задаче Дирихле, служит определение температуры внутри пластинки при известных ее значениях на контуре.

Из других физических задач возникла формулировка задачи Неймана. Найти гармоническую в области D ⁺ функцию U (z ) по заданным значениям ее нормальной производной на , а также смешанной задачи Дирихле-Неймана.

Найти гармоническую в D ⁺ функцию по известным ее значениям на некоторых дугах границы и значениям нормальной производной на остальной части .

Смешанная задача встречается главным образом в гидродинамике. Различные приложения этих задач можно найти, например, в книге Лаврентьев И.А. и Шабат Б.В. [1].

Итак, по многочисленности и разнообразию приложений задача Дирихле занимает исключительное место в математике. К ней непосредственно сводится основная задача в гидродинамике – задача обтекания, задачи кручения и изгиба в теории упругости. С нею же тесно связаны основные задачи статистической теории упругости. Мы будем заниматься плоской задачей, которая представляет для нас особый интерес как по обилию приложений, так и по большей разработанности и эффективности методов решения.

2. Совокупность гармонических функций – это совокупность всех решений уравнения Лапласа

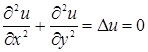, (1)

которое является одним из простейших дифференциальных уравнений с частными производными второго порядка.

Подобно тому, как в случае обыкновенных дифференциальных уравнений для выделения одного определенного решения задают дополнительные условия, так и для полного определения решения уравнения Лапласа требуются дополнительные условия. Для уравнения Лапласа они формулируются в виде так называемых краевых условий, т.е. заданных соотношений, которым должно удовлетворять искомое решение на границе области.

Простейшее из таких условий сводится к заданию значений искомой гармонической функции в каждой точке границы области. Таким образом, мы приходим к первой краевой задаче или задаче Дирихле:

Найти гармоническую в области D и непрерывную в функцию u (z ), которая на границе D принимает заданные непрерывные значения u ().

К задаче Дирихле приводится еще, кроме вышеперечисленных, отыскание температуры теплового поля или потенциала электростатического поля в некоторой области при заданной температуре или потенциале на границе области. К ней сводятся и краевые задачи других типов.

б) Обобщенная задача Дирихле.

В приложениях условие непрерывности граничных значений , является слишком стеснительным и приходится рассматривать обобщенную задачу Дирихле [1]:

На границе области D задана функция , непрерывная всюду, кроме конечного числа точек , где она имеет точки разрыва первого рода. Найти гармоническую и ограниченную в области D функцию u( z) , принимающую значения u( z) = во всех точках непрерывности этой функции.

Если заданная функция непрерывна, то обобщенная задача Дирихле совпадет с обычной, ибо условие ограниченности функции u( z) следует из условия ее непрерывности в .

Теорема единственности решения обобщенной задачи Дирихле: