Реферат: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам
Граничные значения гармонической функции 
на окружности кольца 
мы будем предполагать заданными в форме функций от полярного угла 
и обозначим их соответственно через 
и 
.
Сопряженная с гармоническая функция 
будет вообще говоря, не однозначной, и фкп 
будет состоять из двух слагаемых: однозначной составляющей, могущей быть разложенной в ряд Лорана в кольце, и логарифм 
с вещественным коэффициентом:
, 
. (29)
Отделяя вещественную и мнимую части, мы получим решение поставленной задачи – задачи Дирихле в кольце, но здесь суммируется не так просто.
Существует более компактная и эффективная формула – интегральная формула Вилля для кругового кольца [2], [3].
§3. Интегральная формула Анри Вилля – проблема Дирихле
для кругового кольца (1912).
Пусть в плоскости комплексного переменного дано круговое кольцо 
, ограниченное окружностями
, 
,
где заданное положительное число 
<1.
Требуется найти регулярную и однозначную внутри области 
функцию 
, если известны значения ее вещественной части на границах кольца.
Для случая круга аналогичная задача решается известной формулой Шварца Г. (1869г) (п.1)
, (
, 
),
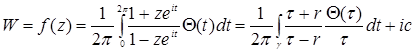где с – действительная переменная.
Здесь предполагается, что радиус круга равен 1, а положение точки на окружности определяется аргументом 
этой точки, так что 
представляет значение вещественной части искомой функции в точке 
.
Нашей задачей является переход от круга к кольцу и построение формулы, аналогичной формуле (1).
Обозначим через 
и 
значения вещественной части искомой функции 
в точках с аргументом на внешней, соответственно внутренней, границе 
.
Основной нашей целью является выяснение того, как скажется на формуле переход от односвязной области к двусвязной.
Величина
,
где интеграл справа берется по окружности радиуса 
(
) с центром в точке 
, очевидно, не зависит от . Тем же свойством обладает и вещественная часть написанного интеграла.
Отсюда, приближая вначале к 1, а замечая, что в интеграле можно
