Реферат: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам

Если L состоит из единственного замкнутого контура, то различают два случая:

а) р= 0. Тогда S⁺ представляет собой конечную часть плоскости, ограниченную контуром ;

б) р= 1, а контур отсутствует. Тогда область S⁺ представляет собой бесконечную часть плоскости, ограниченную контуром .

Легко видеть, что в случае а) задачи А и В совпадают (если считать =0) в случае б) эти задачи непосредственно сводятся одна к другой.

Каждая из задач А и В не может иметь более одного решения (если =0).

д) Общая формулировка задачи Дирихле.

Задача Дирихле – задача отыскания регулярной вобласти D гармонической функции и которая на границе Г области D совпадает с наперед заданной функцией . Задачу отыскания регулярного в области решения эллиптического уравнения 2-го порядка, принимающего на перед заданные значения на границе области, также называется задачей Дирихле, или первой краевой задачей.

Вопросы связанные с этой задачей, рассматривались еще К.Гауссом, а затем Дирихле. Для областей D с достаточно гладкой границей Г решение задачи Дирихле можно представить интегральной формулой

, (8)

где - производная по направлению внутренней нормали в точке функции Грина , характеризуемой следующими свойствами:

1. , при 3 или

, при 2,

где - расстояние между точками и , - площадь единичной сферы в , - регулярная в гармоническая функция как относительно координат , так и относительно координат ;

2. , когда , .

Для шара, полупространства и некоторых других простейших областей функция Грина строится явно и формула (8) дает эффективное решение задачи Дирихле. Получаемые при этом для шара и полупространства формулы носят название формул Пуассона.

Задача Дирихле является одной из основных проблем теории потенциала – теории гармонических функций.

Для обобщенного по Винеру решения задачи Дирихле справедливо интегральное представление в виде формулы Вилля-Пуассона

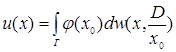, (9)

являющейся обобщением формулы (8). Здесь - гармоническая мера множества в точке . Отсюда возникает возможность рассмотрения обобщенной задачи Дирихле для произвольных граничных функций , при этом можно требовать удовлетворения граничного условия лишь в некоторой ослабленной форме.

Например, если - область с достаточно гладкой границей Г , а граничащая функция имеет только точки разрыва 1-го рода, то можно требовать удовлетворения граничного условия лишь в точках непрерывности , для обеспечения единственности решения в точках разрыва требуется ограниченность решения.

е) Задача Неймана.

Наряду с задачей Дирихле для некоторых приложений важно рассмотреть так называемую вторую краевую задачу, или задачу Неймана:

Найти гармоническую в области функцию , зная значения ее нормальной производной на границе С :

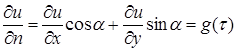(10)

и значение в какой-либо точке в области .

Для определенности мы будем предполагать, что в (10) рассматривается внешняя нормаль, что означает угол, образованный этой нормалью с осью х . Функция может иметь на конечное число точек разрыва 1-го рода, функция и ее частные производные первого порядка предполагаются ограниченными.

Следующая теорема выражает от нормальной производной гармонической функции:

Если функция гармонична в односвязной области и непрерывна вместе со своими частными производными в , то

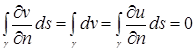, (11)

где - граница области обозначает производную в направлении нормали к , а - дифференциал дуги.

Из этой теоремы следует, что для разрешимости задачи Неймана необходимо выполнения соотношения