Реферат: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам
(![]() ,
, ![]() )
)
Поэтому ![]() представима рядом:
представима рядом:
![]()
![]() (22)
(22)
где ![]() и
и ![]() - коэффициенты Фурье
- коэффициенты Фурье ![]() :
:
![]() ;
; ![]() ;
; ![]()
В центре окружности при ![]() мы получаем:
мы получаем:
![]() (23)
(23)
Равенство (23) – теорема Гаусса о том, что значение гармонической функции в центре окружности есть среднее арифметическое ее значений на самой окружности.
в) Интеграл Пуассона для внешности круга.
Найти функцию, гармоническую и ограниченную вне окружности ![]() и принимающую на самой окружности заданные значения [9]:
и принимающую на самой окружности заданные значения [9]:
![]() ,
, ![]() (
(![]() ).
).
Покажем, что искомую функцию ![]() может быть представлена интегралом типа Пуассрна, который может быть получен из (1).
может быть представлена интегралом типа Пуассрна, который может быть получен из (1).
Пусть ![]() , а
, а ![]() ,
,
Функция ![]() , гармоническая вне окружности
, гармоническая вне окружности ![]() , перейдет в функцию
, перейдет в функцию  , гармоническую внутри круга радиуса
, гармоническую внутри круга радиуса ![]() , принимающую на его границе значения
, принимающую на его границе значения
![]() .
.
По формуле (1) она при ![]() представима интегралом Пуассона:
представима интегралом Пуассона:
 .
.
Если в этом равенстве подставить вместо ![]() и
и ![]() их выражения через
их выражения через ![]() и
и ![]() и заменить переменную интегрирования, положив
и заменить переменную интегрирования, положив ![]() , то мы получим формулу Пуассона для внешности окружности:
, то мы получим формулу Пуассона для внешности окружности:
 , (24)
, (24)
решающую поставленную задачу. Она отличается от (1) только тем, что в ней ![]() и
и ![]() переменились местами, так что ядро интеграла (4) отличается от ядра интеграла Пуассона (1) только знаком.
переменились местами, так что ядро интеграла (4) отличается от ядра интеграла Пуассона (1) только знаком.
Разложение искомой функции в тригонометрический ряд, подобный ряду (22), представляющей ее вне окружности:
![]() . (25)
. (25)
Если в (25) ![]() ®
®![]() , то получим теорему Гаусса для внешности окружности:
, то получим теорему Гаусса для внешности окружности:
![]() , (26)
, (26)
т.е. значение гармонической функции на бесконечности есть среднее арифметическое значений на граничной окружности.
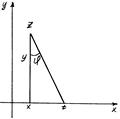
г) Задача Дирихле-Пуассона для полуплоскости.
Аналитический аппарат, позволяющий гармоническую функцию внутри верхней полуплоскости по известным граничным значениям ее вещественной оси, можно получить из интеграла Пуассона путем преобразования круга ![]() плоскости
плоскости ![]() на верхнюю полуплоскость
на верхнюю полуплоскость ![]() при помощи функции
при помощи функции
|
Граничные значения на окружности ![]() перейдут в граничные значения на вещественной оси и мы получим искомую формулу в виде [1]:
перейдут в граничные значения на вещественной оси и мы получим искомую формулу в виде [1]:
|
|
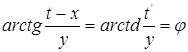 ,
, 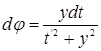
и окончательно имеем: