Реферат: Об интегральных формулах Вилля-Шварца для трехсвязных областей и ее применение к краевым задачам

Доказывается единственность решения задачи Неймана и при доказательстве единственности решения задачи Неймана можно ограничиться случаем, когда область представляет собой полуплоскость (z , > 0).

В дополнительном предположении непрерывности частных производных в решение задачи Неймана сводится к решению задачи Дирихле для сопряженной гармонической функции.

Две гармонические в области функции и , связанные условиями Даламбера-Эйлера называются сопряженными.

Как мы знаем, для всякой функции гармонической в односвязной области , можно найти сопряженную с ней гармоническую функцию . Так как функция определяется своими частными производными с точностью до постоянного слагаемого, то совокупность всех гармонических функций сопряженных с дает формула:

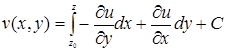, (13)

где С – произвольная действительная постоянная.

Заметим, что в многосвязной области интеграл (13) по контуру , определяет, вообще говоря, многозначную функцию:

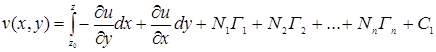, (14)

где - произвольные целые числа, а - интегралы вдоль замкнутых контуров , каждый из которых содержит внутри себя одну связную часть границы :

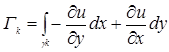. (15)

Постоянные называются периодами интеграла (13) или циклическими постоянными.

Можно доказать, что решение задачи Неймана сводится к решению задачи Дирихле для сопряженной гармонической функции , где , носят название соответственно силовой функции и потенциала поля.

Функции и , представляющие собой регулярные решения системы Коши-Римана [6]:

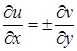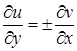
, (16)

имеют частные производные всех порядков, т.е. аналитические функции являются решением уравнения . (17)

Условие (17) – условие комплексной дифференцируемости функции .

§2. О задачах Шварца-Пуассона.

а) Интеграл Шварца для круга

??? ????????, ?? ?????? ????????? ???????????? (??????) ????? ??????? ????????? ? ????????? ?? ????? ??????? ??????????. ????????????? ???????, ?????? ????????? ??????? , ?????????? ? ???????, ????? ???????? ?? ???????, ? ??? ??????, ????? ??????? ???? ???? ??????? , ???????? ? ??? ???? ??? ?????????? ???????? ?????? [6, 8, 9]:

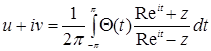, (, ) (18)

Полагая здесь , мы найдем для чисто вещественное значение , для которого мнимая часть обращается в нуль в начале координат.

Чтобы получить общее решение, мы должны добавить к правой части произвольное мнимое число :

, . (19)

Отделим в (18) вещественную и мнимую части, так как вещественная

часть даст нам интеграл Пуассона для и мнимая же часть доставляет выражение через .

Для единичного круга , имеет вид:

, (20)

где , - представляет значение вещественной части искомой функции в точке .

б) Интегральная формула Пуассона.

Задача Дирихле об определении значений гармонической функции внутри круга, если известны ее значения на границе, решается, как известно, интегралом Пуассона:

, (21)

где - полярные координаты точки, где ищется значение решения; - радиус окружности и - функция полярного угла , дающая граничные значения [9].

????? ????????? ??????????? ? ??? ???????, ???