Реферат: Общее понятие определённого интеграла, его геометрический и механический смысл

Этот предел называется определенным интегралом от функции f(x) на отрезке [a, b].

Соответствующее математическое выражение таково:

lim= λ→0

Знак ∫, представляющий растянутую S (начальную букву латинского слова «Summa»), символизирует здесь бесконечное увеличение числа слагаемых интегральной суммы. Буквы a и b, указывающие границы отрезка, на котором выполняется суммирование, называются пределами интегрирования.

Таким образом, определенным интегралом функции от f(x) в границах от a до b называется предел интегральной суммы вида

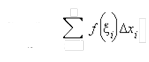
при условии, что длина наибольшего частичного отрезка стремится к нулю.

Выясним теперь возможность непосредственного использования операции, которая привела к понятию определенного интеграла, для решения соответствующих задач. Ограничимся при этом двумя примерами на вычисление площадей.

Пример 1.

Вычислить площадь, заключенную между прямой y=x, осью Ox и прямой x=1.

Решение. Так как данная прямая пересекается с Ox в начале координат, то отрезок интегрирования здесь будет [0, 1].

1). Разбиением этого отрезка на n равных между собой частей получим точки деления с абсциссами:

2). В каждом из полученных n отрезков выберем правые концы, т.е.

Так как f(x) = x, то

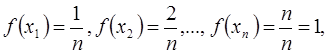
и слагаемые интегральной суммы выразятся в виде

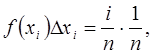
где i – номер элементарного отрезка и принимает значения от 1 до n.

3). Интегральная сумма выразится в виде

(здесь применена формула n членов арифметической прогрессии).

4). Находим предел этой суммы при n → ∞:

Таким образом, искомая площадь равна 1/2 кв.ед. Проведенное вычисление, явно невыгодное из-за своей громоздкости, знакомит с операцией, составляющей сущность определенного интеграла.

Пример 2.