Реферат: Общее понятие определённого интеграла, его геометрический и механический смысл
Решение.
1). Разбивая отрезок интегрирования [0, 1] на n равных частей, получим такие же абсциссы точек деления, как в примере 1.
2). В каждом из частичных отрезков выберем снова правые концы:
![]()
Так как f(x) = x2 , то
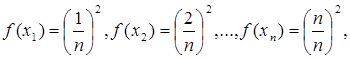
и слагаемые интегральной суммы выразятся в виде
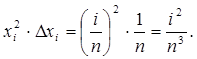
3). Интегральная сумма
![]()
Помещенная в скобках сумма квадратов первых n чисел натурального ряда может быть преобразована по формуле, доказываемой в элементарной алгебре:
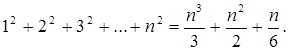
Отсюда
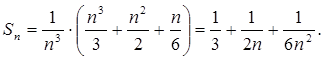
4). Переход к пределу интегральной суммы при n → ∞ дает S = 1/3. Таким образом, искомая площадь равна 1/3 кв.ед.
Выполненное в этих двух примерах непосредственное вычисление определенных интегралов как пределов интегральных сумм
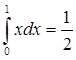 и
и 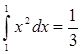
оказалось возможным только благодаря простой структуре операции суммирования, да и то оно потребовало проведения сложных подсчетов. Надо отметить, что такие приемы вычисления (здесь применен способ Архимеда) существовали до появления понятия интеграла.
Поэтому естественным развитием понятия определенного интеграла является выбор целесообразного способа его вычисления. Такой способ, оказывается, дает операция интегрирования ввиду наличия связи между определенным интегралом и интегралом неопределенным.
Связь между определенным и неопределенным интегралами. Формула Ньютона-Лейбница
Рассмотрим криволинейную трапецию (рис. 2), у которой правая граничная прямая не зафиксирована. Площадь этой трапеции измеряется переменной величиной, зависящей от положения ее правой границы х. Пусть это будет некоторая функция Φ(х). Тогда справедлива следующая теорема.
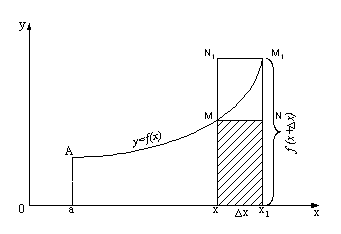 |
Рис. 2
Теорема. Функция Φ(х), выражающая площадь переменной криволинейной трапеции (с подвижной правой стороной), является первообразной для функции y = f(х), графиком которой является кривая, ограничивающая эту же трапецию сверху.
По смыслу определения первообразной запись
Φ(х) = ∫f(х)dx
будет оправдана, если мы докажем, что
Φ'(х) = f(х).
Доказательство. Дадим начальному значению х приращение Δх. Тогда функция, выражающая площадь криволинейной трапеции, получит приращение
ΔΦ(х) = пл. хММ1 х1 ,.
Это приращение площади (рис. 2) больше площади прямоугольника хМNх1 , равной f(х)Δх, и меньше площади прямоугольника xN1 M1 x1 , равной