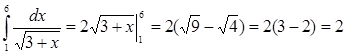Реферат: Общее понятие определённого интеграла, его геометрический и механический смысл

Деление всех членов неравенств на Δх > 0 дает

f(х) < < f(х+ Δх).

Если теперь ввести условие Δх → 0, то в силу непрерывности функции

у= f(х)

Таким образом, отношение заключено между двумя переменными, имеющими общий предел при Δх → 0. Но из этого следует,

что ,

т.е. Φ'(х) = f(х).

Этим доказано, что функция Φ(х), выражающая площадь криволинейной трапеции, является первообразной для f(х).

Выражение этой функции возможно в двоякой форме.

Исходя из того, что рассмотренная ранее задача о площади криволинейной трапеции (с фиксированными границами) получает свое разрешение с помощью определенного интеграла, можно записать

пл. aABb =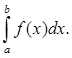

Вместе с тем эта же площадь может быть выражена как частное значение функции Φ(х) при x = b, и тогда

Φ(b) = 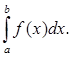(1)

Аналогично площадь криволинейной трапеции (рис. 2) с переменной правой границей х выражается в виде

Φ(х) = 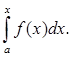(2)

Этот интеграл оказывается функцией от верхнего предела.

С другой стороны, если Φ(х), выражающая площадь aAMx, является первообразной для функции f(х), то можно представить ее в виде Φ(х)=F(х)+C, где F(х) – некоторая первообразная для той же функции.

Приравнивая первые части равенств (1) и (2), получаем

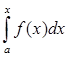= F(х) + C.

Для определения постоянной С используем то, что при х = а трапеция превращается в отрезок, и ее площадь оказывается равной нулю, т.е.

Φ(а) = F(а) + C = 0,

а отсюда С = − F(а) и, следовательно,

Φ(х) = 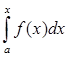= F(х) − F(а).

Давая аргументу х значение фиксированного верхнего предела, т.е. при x = b, мы получаем выражение определенного интеграла через значения первообразной в виде следующей формулы:

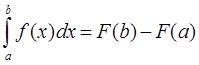Это – формула Ньютона-Лейбница. Она связывает определенный интеграл с неопределенным.

Для вычисления определенного интеграла эта формула обычно записывается в виде

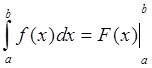где знак служит символическим обозначением разности между значениями первообразной функции F(b) и F(а).

Пример 1.