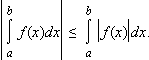Реферат: Общее понятие определённого интеграла, его геометрический и механический смысл

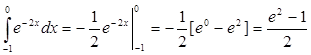
Пример 3.

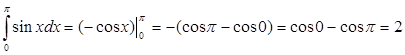
Таким образом, формула Ньютона-Лейбница используется для вычисления определенного интеграла так:

1). Находится первообразная для данной подынтегральной функции.

2). Вычисляются частные значения первообразной подстановкой значений x = a и x = b, где b – верхний и a – нижний пределы интегрирования.

3). Определяется разность частных значений первообразной F(b) – F(а).

Свойства определенного интеграла

Доопределим понятие определенного интеграла при a ≥ b следующими равенствами:

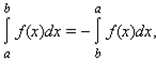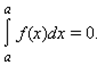Сформулируем некоторые свойства определенного интеграла в предположении, что подынтегральная функция ограничена на отрезке, по которому она интегрируется.

1). Если функция интегрируема на [a; b], то она интегрируема на

любом отрезке [x₁ ; x₂ ] [a; b].

2). Для любых a, b и c

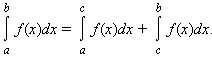
3). Интеграл обладает свойством линейности: для любых функций f(x) и g(x) и любой постоянной A

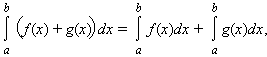
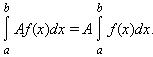
4). Если f(x) и g(x) интегрируемы на [a; b], то f(x) · g(x) также интегрируема на этом отрезке.

5). Если f(x) – периодическая функция с периодом T, то для любого a

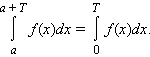
Для определенных интегралов верны также следующие оценки (предполагается, что функции f и g интегрируемы на [a; b]).

1). Если f(x) ≥ g(x), то

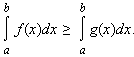
2). В частности, если f(x) ≥ 0, то

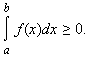
3). Если f(x) ≥ 0 для любого х [a; b] и существует х₀ [a; b] такое, что f(x₀ )>0, причем f(x) непрерывна в х₀ то

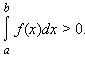
4). |f(x)| интегрируема на [a; b], причем