Реферат: Основні властивості простору Соболєва
 при
при ![]()
З умови фундаментальності в середньому ![]() в
в ![]() треба, що окремо при
треба, що окремо при ![]()

Аналогічно, з умови еквівалентності ![]() й
й ![]() по нормі
по нормі ![]() треба, що при
треба, що при ![]()

Відповідно до визначення простору ![]() існують функції
існують функції ![]() й
й ![]() такі, що при
такі, що при ![]()
![]() а
а ![]() в середньому.
в середньому.
Ми приходимо до наступного найважливішого визначення. Нехай ![]() Тоді у
Тоді у ![]() визначені елемент
визначені елемент ![]() із представником
із представником ![]() і елемент
і елемент ![]() із представником
із представником ![]()
![]() називається узагальненій похідній (у змісті Соболєва) від
називається узагальненій похідній (у змісті Соболєва) від ![]() При цьому пишуть:
При цьому пишуть: ![]()
З визначення узагальненій похідній ![]() видно, що вона визначається не локально, в окремих крапках, а глобально – відразу на всім відрізку
видно, що вона визначається не локально, в окремих крапках, а глобально – відразу на всім відрізку ![]() Нехай
Нехай ![]() так що
так що ![]()
![]() Перейдемо до межі при
Перейдемо до межі при ![]() в рівностях
в рівностях
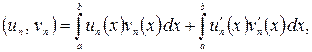 (1.4)
(1.4)
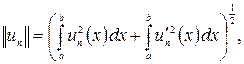 (1.5)
(1.5)
і, відповідно до теореми про поповнення й визначення інтеграла Лебега, прийдемо до формул (1.2) і (1.3), де тепер похідні розуміються в узагальненому змісті, а інтеграл – у змісті Лебега. Для конкретних обчислень, зрозуміло, можна й потрібно користуватися формулами (1.4) і (1.5), взявши досить велике ![]() тобто замість ідеальних елементів
тобто замість ідеальних елементів ![]()
![]()
![]()
![]() скористатися їхніми гладкими наближеннями
скористатися їхніми гладкими наближеннями ![]()
![]()
![]()
![]()
1.3 Інше визначення узагальненої похідної
Нехай ![]() – множина всіх безупинно диференцюємих на відрізку
– множина всіх безупинно диференцюємих на відрізку ![]() фінітних функцій
фінітних функцій ![]() Якщо тепер
Якщо тепер ![]() безупинно дференцюєма на відрізку
безупинно дференцюєма на відрізку ![]() те для довільної функції
те для довільної функції ![]() справедливо наступна інтегральна тотожність:
справедливо наступна інтегральна тотожність:
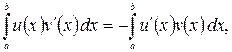 (1.6)
(1.6)
перевіряється інтегруванням вроздріб. Цією тотожністю ![]() повністю визначається.
повністю визначається.
Допустимо, що, крім того, для будь-яких ![]() і деякої безперервної на відрізку
і деякої безперервної на відрізку ![]() функції
функції ![]()
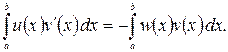 (1.7)
(1.7)
Віднімаючи ці тотожності, одержимо, що для будь-яких ![]()
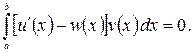
Звідси, внаслідок щільності ![]() в
в ![]()
![]() на відрізку
на відрізку ![]() Виявляється, інтегральна тотожність (1.7) можна прийняти за визначення узагальненої похідної. Насамперед, справедлива наступна лема.
Виявляється, інтегральна тотожність (1.7) можна прийняти за визначення узагальненої похідної. Насамперед, справедлива наступна лема.
Лема 1. Якщо ![]() то для будь-яких
то для будь-яких ![]() справедливо тотожність (1.6).
справедливо тотожність (1.6).
Доказ. Нехай ![]() тоді для всіх
тоді для всіх ![]() маємо (1.6):
маємо (1.6):
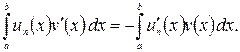
Внаслідок властивості безперервності скалярного добутку в останній рівності можна перейти до межі при ![]() В результаті ми одержимо тотожність (1.6) для будь-якої функції
В результаті ми одержимо тотожність (1.6) для будь-якої функції ![]() Лема доведена.
Лема доведена.
Лема 2. Нехай дані ![]()
![]() такі, що для всіх
такі, що для всіх ![]() справедливо тотожність (1.7). Тоді
справедливо тотожність (1.7). Тоді ![]() (узагальнена похідна).
(узагальнена похідна).
Доказ. Нехай ![]() а
а ![]() Тоді
Тоді
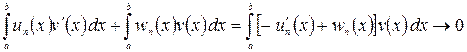
при ![]()
для будь-якого ![]()