Реферат: Основні властивості простору Соболєва

Елементи називаються узагальненими частками похідними елемента

Скалярний добуток і норма задаються в тими ж формулами, що й в у які тепер похідні узагальнені, а інтегрування розуміється в змісті Лебега. Уведемо в розгляд простір Цей простір є поповненням у нормі

(1.10)

лінійного простору функцій, безупинно диференцюємих на й таких, що є гильбертовим простором зі скалярним добутком

Лема 3. Якщо а те

Доказ. Досить довести першу із цих формул. Вона справедлива, якщо а Нехай – фундаментальна в послідовність, межу якої – елемент Переходячи в тотожності до межі при одержимо для будь-який Дійсно, зі збіжності в треба, що

тобто безперервність скалярного добутку.

Нехай тепер – фундаментальна послідовність у Перейдемо до межі в тотожності

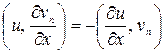
й одержимо вихідну тотожність.

Наслідок. утримується строго усередині

Дійсно, функція Але інакше ми мали б

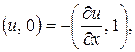
тобто

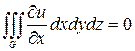
для кожної Візьмемо й одержимо протиріччя.

Теорема 2 (Фридрихс). Існує постійна така, що для будь-яких

Доказ. По самому визначенню всякий елемент із належить Нехай і сходиться в до

Побудуємо куб

утримуючу область Функції визначимо нулем у Частинна похідна існує всюди в за винятком, бути може, тих крапок, у яких пряма, паралельна осі абсцис, перетинає границю області Для будь-якої крапки маємо

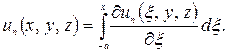
По нерівності Коші-Буняковського