Реферат: Основні властивості простору Соболєва

Тоді

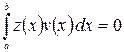
для будь-яких Звідси Лема доведена.

1.4 Найпростіша теорема вкладення

Теорема 1. вкладено в

Доказ. Нехай безупинно дференцюєма на відрізку Відповідно до теореми про середній, внаслідок безперервності найдеться крапка така, що 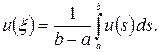Тому на відрізку справедливо наступна тотожність:

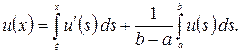
За допомогою нерівності Коші-Буняковського маємо

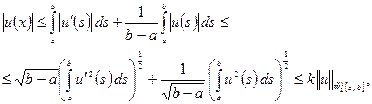
де

Отже, для будь-який безупинно дференцюємої на відрізку функції справедлива нерівність

(1.8)

Нехай тепер послідовність – фундаментальна по нормі Тоді

при Отже, фундаментальна в змісті рівномірної збіжності й, за критерієм Коші рівномірної збіжності, сходиться до Тим більше в середньому. Таким чином, у класі з утримуючої як представник, утримується безперервна функція й, виходить, цей клас можна ототожнити з Ототожнимо елементи з безперервними функціями. Нехай Переходячи в нерівності до межі при прийдемо до нерівності (1.8).

Отже, вкладення в доведено. Доказ теореми закінчений.

1.5 Простір Соболєва й

Нехай – однозв'язна область із досить гладкою границею В замкнутій області розглянемо лінійний простір усіляких безупинно диференцюємих функцій зі скалярним добутком

При цьому

(1.9)

Отриманий простір зі скалярним добутком позначається а його поповнення – це, по визначенню, простір Соболєва

Нехай – фундаментальна послідовність у тобто при Звідси треба, що в будуть фундаментальними послідовності

Внаслідок повноти в є елементи, які ми позначимо

так що при в середньому