Реферат: Основні властивості простору Соболєва

Інтегруючи отриману нерівність по знаходимо

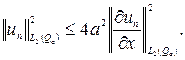
Тому що поза те

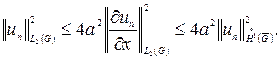
Переходячи до межі при приходимо до доказуваної нерівності Фридрихса.

Наслідок 1. Простір вкладений в

Це пропозиція безпосередньо випливає з визначення вкладення банахових просторів і нерівності Фридрихса.

Наслідок 2. У норми (1.9) і (1.10) еквівалентні.

Дійсно, використовуючи нерівність Фридрихса, маємо

2. Застосування просторів Соболєва в математичній фізиці

2.1 Доказ існування й одиничності узагальненого рішення рівняння Лапласа

Теорема 3 (Рисс). Нехай – гильбертовий простір. Для будь-якого лінійного обмеженого функціонала заданого всюди на існує єдиний елемент такий, що для всіх

При цьому

Доказ наведений в [1, стор. 171].

Теорема Рисса ефективно застосовується в теорії можливості розв'язання граничних задач для рівнянь із частками похідними. Будемо говорити, що гильбертовий простір вкладений у гильбертовий простір якщо із треба, що причому існує постійна така, що для всіх

(2.1)

Має місце наступний наслідок з теореми Рисса.

Теорема 4. Якщо гильбертовий простір вкладений у гильбертовий простір то для кожного елемента найдеться єдиний елемент такий, що для всіх має місце тотожність

Тотожність це визначає оператор такий, що при цьому

Доказ. При кожному фіксованому вираження при всіляких визначає лінійний обмежений функціонал на Лінійність функціонала очевидна. Його обмеженість випливає з оцінки

По теоремі Рисса існує єдиний елемент такий, що Тим самим усюди на заданий лінійний оператор Далі, з доведеного вище нерівності треба, що

Думаючи тут одержимо тобто й, виходить, обмежений. Теорема доведена.

Як додаток доведеної теореми й просторів Соболєва доведемо існування й одиничність узагальненого рішення задачі Дирихле для рівняння Пуассона. У замкнутої обмеженої однозв'язної області з досить гладкою границею розглянемо наступну граничну задачу:

(2.2)

(2.3)

Припустимо, що права частина безперервна в по сукупності змінних. Функція називається класичним рішенням задачі (2.2) – (2.3), якщо безперервно як функцію трьох змінних у має в безперервні похідні, що входять у ліву частину (2.2), задовольняє в рівнянню (2.2) і дорівнює нулю на тобто задовольняє граничній умові (2.3).