Реферат: Похідні та диференціали функції багатьох змінних
Повним диференціалом ![]() диференційовної в точці
диференційовної в точці ![]() функції
функції ![]() називається лінійна відносно
називається лінійна відносно ![]() та
та ![]() частина повного приросту цієї функції в точці M, тобто
частина повного приросту цієї функції в точці M, тобто
![]() . (3)
. (3)
Диференціалами незалежних змінних x та ![]() назвемо прирости цих змінних
назвемо прирости цих змінних![]() . Тоді з урахуванням теореми 2 рівність (3) можна записати так:
. Тоді з урахуванням теореми 2 рівність (3) можна записати так:
 . (4)
. (4)
Аналогічна формула має місце для диференційовної функції трьох змінних![]() :
:
 . (5)
. (5)
З формул (4) і (5) може здатися, що повний диференціал ![]() існуватиме у кожній точці, в якій існують частинні похідні. Але це не так. Згідно з означенням, повний диференціал можна розглядати лише стосовно диференційовної функції.
існуватиме у кожній точці, в якій існують частинні похідні. Але це не так. Згідно з означенням, повний диференціал можна розглядати лише стосовно диференційовної функції.
Теореми та формули для диференціалів функції однієї змінної повністю зберігаються і для диференціалів функцій двох, трьох і т.д. змінних . Так, незалежно від того, від яких аргументів залежать функції u і ![]() , завжди справедливі рівності
, завжди справедливі рівності
![]()
![]()
![]()
![]()
Покажемо, що різниця між повним приростом ![]() і диференціалом
і диференціалом ![]() при
при ![]() і
і ![]() є нескінченно мала величина вищого порядку, ніж величина
є нескінченно мала величина вищого порядку, ніж величина![]() .
.
Дійсно, з формул (1) і (3) маємо
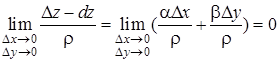 ,
,
оскільки функції ![]() – нескінченно малі при
– нескінченно малі при![]() ,
, ![]() , а
, а ![]() та
та ![]() – обмежені функції:
– обмежені функції:
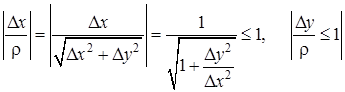 .
.
Отже, різниця ![]() – нескінченно мала величина вищого порядку, ніж
– нескінченно мала величина вищого порядку, ніж![]() . Тому повний диференціал називають також головною частиною повного приросту диференційовної функції. При цьому виконується наближена рівність
. Тому повний диференціал називають також головною частиною повного приросту диференційовної функції. При цьому виконується наближена рівність ![]() або
або
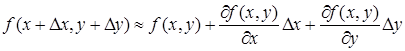 . (6)
. (6)
Ця рівність тим точніша, чим менша величина![]() . Рівність (6) широко використовується у наближених обчисленнях, оскільки диференціал функції обчислюється простіше, ніж повний приріст.
. Рівність (6) широко використовується у наближених обчисленнях, оскільки диференціал функції обчислюється простіше, ніж повний приріст.
Покажемо, як за допомогою диференціала можна оцінити похибку в обчисленнях.
Нехай задана диференційовна функція![]() , незалежні змінні якої виміряні з точністю
, незалежні змінні якої виміряні з точністю![]() . Потрібно знайти похибку, з якою обчислюється u.
. Потрібно знайти похибку, з якою обчислюється u.
Природно вважати, що ця похибка дорівнює величині
![]() .
.
Для малих значень ![]() маємо
маємо
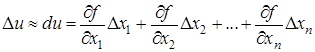 ,
,
звідки
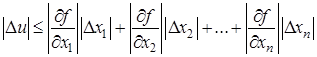 .
.
Якщо через ![]() позначити максимальну абсолютну похибку змінної
позначити максимальну абсолютну похибку змінної![]() , то можна отримати значення максимальної абсолютної похибки
, то можна отримати значення максимальної абсолютної похибки ![]() функції
функції ![]() :
: