Реферат: Похідні та диференціали функції багатьох змінних

1 Частинні похідні

Нехай функція визначена в деякому околі точки .
Надамо змінній x приросту, залишаючи змінну незмінною, так, щоб точка належала заданому околу.

Величина

називається частинним приростом функції за змінноюx.

Аналогічно вводиться частинний приріст функції за змінною:

.

Якщо існує границя

,

то вона називається частинною похідною функції в точці за змінною x і позначається одним із таких символів:

.

Аналогічно частинна похідна функції за визначається як границя

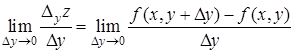
і позначається одним із символів:

.

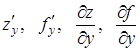Згідно з означенням при знаходженні частинної похідної обчислюють звичайну похідну функції однієї змінної x, вважаючи змінну сталою, а при знаходженні похідної сталою вважається змінна x. Тому частинні похідні знаходять за формулами і правилами обчислення похідних функцій однієї змінної.

Частинна похідна (або) характеризує швидкість зміни функції в напрямі осі (або).

З’ясуємо геометричний зміст частинних похідних функції двох змінних. Графіком функції є деяка поверхня (рис 1). Графіком функції є лінія перетину цієї поверхні з площиною. Виходячи з геометричного змісту похідної для функції однієї змінної, отримаємо, що, де– кут між віссю і дотичною, проведеною до кривої в точці. Аналогічно.

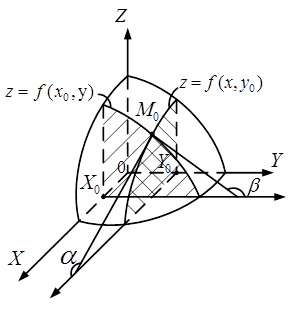
Рисунок 1 – Геометричний зміст частинних похідних

Для функції n змінних можна знайти n частинних похідних:

,

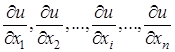де

,

.

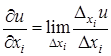Щоб знайти частинну похідну, необхідно взяти звичайну похідну функції за змінною, вважаючи решту змінних сталими.

Якщо функція задана в області і має частинні похідні в усіх точках, то ці похідні можна розглядати як нові функції, задані в області.

Якщо існує частинна похідна за x від функції, то її називають частинною похідною другого порядку від функції за змінною x і позначають або .

Таким чином, за означенням

--> ЧИТАТЬ ПОЛНОСТЬЮ <--