Реферат: Поняття фракталів

ІІ Основна частина

2.1 Класифікація алгоритмів створення фракталів

Бенуа Мандельброт в своїх книгах навів яскраві приклади вживання фракталів до пояснення деяких природних явищ. Мандельброт приділив велику увагу цікавій властивості, якою володіють багато фракталів. Річ у тому, що часто фрактал можна розбити на скільки завгодно малі частини так, що кожна частина виявиться просто зменшеною копією цілого. Інакше кажучи, якщо ми дивитимемося на фрактал в мікроскоп, то із здивуванням побачимо ту ж саму картину, що і без мікроскопа. Це властивість самоподібності різко відрізняє фрактали від об'єктів класичної геометрії.

Необхідно відзначити, що властивість самоподiбностi характерна лише для регулярних фракталів.Багато регулярних фракталів будуються шляхом нескiнченного повторення декількох простих операцій - заміною одного елементу деякою комбінацією інших, йому подібних. Потім ця ж операція повторюється з кожним з цих елементів, і так далі до нескінченності. На методі простої заміни заснований перший алгоритм побудови фракталів.

Виникає питання, чи не можна цю "процедуру заміни" перекласти мовою математичних формул. Таким чином, в середині 80-х років з'явився метод Систем Ітеріруємих Функцій - СІФ (Iterated Function System - IFS) як простий засіб здобуття фрактальних структур. Таким чином, деякі з вищеперелічених фракталів можна отримати за допомогою методу СІФ. Метод Систем Ітеріруємих функцій є основою для другого алгоритму побудови фрактальних структур. Замість детермінованого способу побудови регулярних фракталів в алгоритм створення фрактальних структур був включений деякий елемент випадковості, що приводить до побудови випадкових фракталів. Багато фракталів можуть бути отримані за допомогою цих двох алгоритмів. Тоді в першому випадку вони побудовані як регулярні фрактали, а в другому як випадкові.

Одним з найбільш яскравих прикладів серед різних систем ітеріруємих функцій є відкрита система М. Бранслі з чотирьох стискуючих афінних перетворень, аттрактором для якої є множина точок, яка дуже нагадує по формі зображення листа папороті.

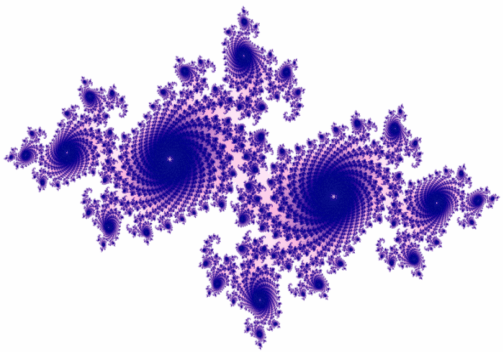
Мал.7

Третім алгоритмом створення фрактальних об'єктів на площині є використання комплексних відображень, що зіставляють одному комплексному числу інше комплексне число за деяким ітераційним правилом. Прикладом фрактала отриманого за допомогою комплексних відображень є множина Жюліа (мал.7).

2.2 Системи Ітеріруємих Функцій

У евклідовом просторі відстань (x;y) між точками x=(;) і y=(;) визначається за допомогою наступної формули

Відстань в просторі можна також вимірювати функцією (x;y)=|-|+|-|.

Дві приведені функції, будучи вимірами відстані, по-різному визначають відстані між двома точками. Існують чотири основні властивості функції відстані:

- відстані від точки x до точки y і від точки y до точки x рівні: d(x;y)=d(у;x);

- відстань від точки x до цієї ж точки x дорівнює нулю: d(x;x)=0;

- відстань по прямій - це найкоротша відстань між двома точками: d(x;y) <=d(x;z)+d(z;y);

- для двох точок x і у функція відстані має бути дійсною, скінченою і додатною : .

Функція відстані, що задовольняє даним властивостям, називається метрика .

Метричний простір (X,d) - множина точок X разом з метрикою d, визначеною на X.

Перетворення - зіставлення, згідно заздалегідь визначеному правилу, точці в одному просторі точки в іншому (можливо і в тому ж самому просторі).

Відображення , це перетворення, яке переводить простір X₁ в простір X₂ і позначається f_n : X₁ X₂ .

Стиснююче відображення - перетворення в метричному просторі X₁ X₂ за умови існування коефіцієнта стиснення перетворення f: 0s<1 такого, що d(f(x₁ ),f(x₂ )) sd(x₁ ,x₂ ) для всіх

Система ітеріруємих функцій (Iterated Function System) складається з повного метричного простору (X,d) і скінченної множини стиснюючих відображень f_n : X₁ X₂ з коефіцієнтами стиснення Sn.

2.3 Стиснюючі афінні перетворення

Мал. 8.

Перш ніж розкривати зміст поняття - стиснюючі афінні перетворення, розглянемо лінійне перетворення на комплексній площині Z, яке переводить рівносторонній трикутник з довжиною сторони рівній одиниці в рівносторонній трикутник в два рази меншого розміру представлений на мал. 8.