Реферат: Преобразование Лапласа

тогда обратное преобразование существует и соответствующее прямое преобразование имеет абсциссу абсолютной сходимости.

Примечание: это достаточные условия существования.

· Теорема о свёртке

Преобразованием Лапласа свёртки двух оригиналов является произведение изображений этих оригиналов.

· Умножение изображений

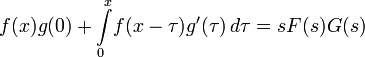
Левая часть этого выражения называется интегралом Дюамеля, играющим важную роль в теории динамических систем.

· Дифференцирование и интегрирование оригинала

Изображением по Лапласу первой производной от оригинала по аргументу является произведение изображения на аргумент последнего за вычетом оригинала в нуле справа.

В более общем случае (производная n-го порядка):

Изображением по Лапласу интеграла от оригинала по аргументу является изображение оригинала деленное на свой аргумент.

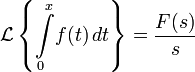
· Дифференцирование и интегрирование изображения. Обратное преобразование Лапласа от производной изображения по аргументу есть произведение оригинала на свой аргумент, взятое с обратным знаком.

Обратное преобразование Лапласа от интеграла изображения по аргументу есть оригинал этого изображения, деленный на свой аргумент.

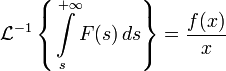
· Запаздывание оригиналов и изображений. Предельные теоремы

Запаздывание изображения:

Запаздывание оригинала:

Примечание: u(x) — Функция Хэвисайда.

Теоремы о начальном и конечном значении (предельные теоремы):