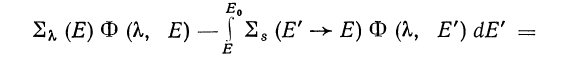Реферат: Преобразование Лапласа

быстро убывает с ростом Q экспоненту в (4) можно разложить в ряд.

Тогда

где -середина потери энергии на единице длины пути. Подставим это разложение в (6) и сделаем замену переменных

Тогда (6) перейдет в:

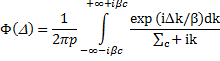
Вычисляя, интеграл с помощью вычетов и возвращаясь от переменной к переменной E, получаем:

(7)

Экспонента в формуле (7) есть вероятность того, что частица избежит поглощения на пути, где энергия меняется от Е₀ до Е. Если сечение поглощения равно нулю, то

(8)

Формула (8) имеет простой физический смысл. По определению Ф(E)=dE есть средний путь, пройденный частицей за время, пока ее энергия меняется от E+dE до E.

В приближении непрерывного замедления dE/dl=b, откуда dl/dE=1/b, что совпадает с (8).

10. Преобразование Лапласа по координатам

Запишем кинетическое уравнение в приближении «прямо-вперед» (т.е. без учета отклонения частиц при рассеянии), для частиц, испускаемых моноэнергетическим источником, который находится в начале координат:

(208)

(209)

Поскольку частицы испускаются в положительном направлении оси Оz, в области z<0 плотность потока равна 0 и область изменения z в уравнении (208) следует считать полубесконечный интервал (0,¥). Это обстоятельство позволяет применить для решения уравнения (208) преобразование Лапласа по координатам:

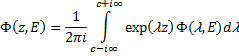(210)

где трансформанта Лапласа Ф(l,E) выражается через плотность потока следующим образом:

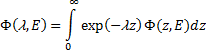(211)

Умножим обе части уравнения (208) на и проинтегрируем по z от 0 до ¥. Преобразовав первый член интегрированием по частям с учетом граничного условия (209) и, использовав обозначение (211), получим:

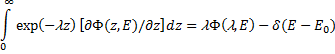
После преобразования Лапласа остальных членов уравнения (208) приходим к уравнению для трансформанты плотности потока:

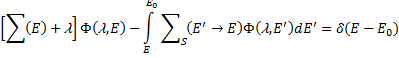(212)

которое в отличие от (208) не содержит производных и является интегральным уравнением типа уравнения деградации энергии. Введя обозначение

(213)

Перепишем уравнение (312) в виде