Реферат: Преобразование Лапласа

При действительных уравнение (214) по форме совпадает с уравнением деградации энергии для частиц с макроскопическим сечением столкновений и дифференциальным сечением рассеяния

Из (213) видно, что по мере уменьшения lобращается в нуль, а потом становится отрицательной. Отсюда следует, что решение уравнения (214) существует лишь в области

Если выполняется условие

то для трансформанты рассеянной компоненты плотности потока получим

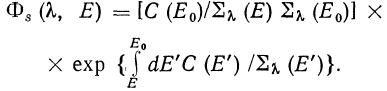(215)

Если и C не зависят от энергии, формула (215) упрощается:

(216)

Перейдем к восстановлению энергетического спектра рассеянных частиц:

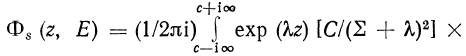
(217)

гдеRel=C>-

Введем обозначения

Тогда формула (217) примет вид:

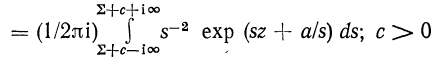(218)

Функция , представляющая собой обратное преобразование Лапласа функции s^-2 exp(a/s),равна

'

где I₁ - модифицированная функция Бесселя первого порядка. Таким образом

(219)

В частности, при малых значениях аргумента I₁ (x), поэтому

(220)

При больших значениях аргумента , следовательно,

(221)