Реферат: Преобразование Лапласа

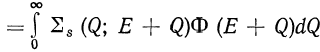
и, не пренебрегая для простоты зависимостью сечений Σ(E) и

от E, перейдем от E к новой переменной

D=:

Ф(D)=Ф(E)(1)

Решение этого уравнения можно получить с помощью преобразования Лапласа по энергии:

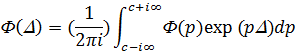(2)

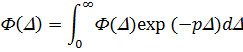(3)

Его можно рассматривать как разложение дифференциальной плотности потока по системе биортогональной функции и .

Подействуем на все члены уравнения (1) оператором

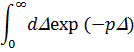
В соответствии с (3) первый член преобразования к виде

Во втором члене необходимо изменить порядок интегрирования и в интеграле по D сделать замену переменных

Тогда он приведется к виду

,

где (4)

-трансформанта Лапласа от дифференциального сечения рассеяния.

Правая часть уравнения (1) легко преобразуется, после чего получаем

’

Откуда

. (5)

Подставляя (5) в (2), находим интересующую нас функцию Ф(D):

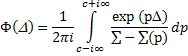
Если сечение