Реферат: Прикладная математика

a_ij – норма времени на обработку единицы i -го изделия на j -ой группе оборудования;

b_i – действительный фонд времени работы i -й группы оборудования;

x_i – планируемое количество единиц j -го изделия;

(x₁ , x₂ , … , x_n ) – искомый план производства.

Какова бы ни была производственная программа (x₁ , x₂ , … , x_n ), ее компоненты должны удовлетворять условию, что суммарное время обработки всех изделий на данной группе оборудования не должно превышать фонда времени работы этой группы оборудования. На обработку x₁ единиц первого изделия на i -й группе оборудования будет затрачено a_i1 x₁ единиц времени, на обработку x₂ единиц второго изделия на той же группе оборудования будет затрачено a_i2 x₂ единиц времени и т.д. Необходимое время на обработку всех x₁ , x₂ , … , x_n изделий на i -й группе оборудования будет равно сумме

Эта сумма не может превышать фонд времени работы i -й группы оборудования, т.е. должна быть £ b_i . Выписывая такие условия для всех m групп оборудования, получаем:

(1)

Так как компоненты плана суть количество изделий и, следовательно, не могут быть выражены отрицательными числами, то естественным образом добавляются условия:

x₁ ³0, x₂ , ³0,…, x_n ³0.

(2)

Обозначим через с _j прибыль на единицу j-го изделия. При плане производства (х₁ , х₂ , …, х_n )прибыль предприятия будет равна:

z = c₁ x₁ + c₂ x₂ + … + c_n x_n . (3)

Мы хотим составить производственную программу (х₁ , х₂ , …, х_n ) так, чтобы функция (3) приняла наибольшее значение при выполнении всех других условий.

9

??????? ???????? ?????????? (1), (2) ? ???????? ????? (3) ???????? ?????????????? ?????? ?????? ? ???????????? ????????????? ???????????????? ?????????. ????? ???? ??????? ??????? ???????? ?????????? (1), ??????????????? ??????? ????????????????? (2), ?????????? ????? ????? ???????, ??? ??????? ???????? ????? (3) ????????? ?????????? ????????? ????????. ??? ? ?????? ????????? ????????????????.

Исходные параметры задачи могут быть представлены в виде технологической матрицы A затрат ресурсов на единицу продукции каждого вида, вектора B объемов ресурсов и вектора C удельной прибыли:

, , C=(c₁ , …, c_n )

В качестве примера рассмотрим задачу оптимизации производственной программы цеха, который может выпускать два вида изделий, имея четыре группы производственного оборудования. Пусть

, , , или кратко

Задача состоит в том, чтобы найти производственную программу, максимизирующую

прибыль:

(4)

при условиях:

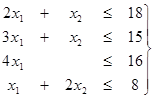(5)

(6)

10

?????????? ?????? ????????? ???????????????? ? ????? ??????????? ????? ?????? ??????????. ??????? ???????? ?????????? (5), (6) ?????????? ???????? ????????????? OPQRS ?????????? ???????. ????? ?????? ??????? Z ??????????????? ???????-????????? grad Z =(6,9) ? ???????? ????????? ???????????? ?????? (???????? ????????? ??????????? ??????????? ???????). ??????????? ???????? ??????? Z ????????? ? ????? R . ?????????? ???? ????? ?????????? ??????????? ???? ???????????? x₁ =3, x₂ =2, ? ???????????? ??????? ????? ????? 36.

Последовательное улучшение производственной программы

Предположим теперь, что предприятие может выпускать четыре вида продукции, используя для этого три вида ресурсов. Известна технологическая матрица А затрат любого ресурса на единицу каждой продукции, вектор В объемов ресурсов и вектор С удельной прибыли

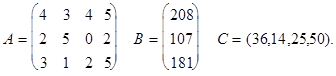(7)

Требуется составить производственную программу, обеспечивающую предприятию наибольшую прибыль при имеющихся ограниченных ресурсах

Математическая модель задачи:

найти производственную программу

(x₁ , x₂ , x₃ , x₄ )

максимизирующую прибыль