Реферат: Прикладная математика

при ограничениях по ресурсам

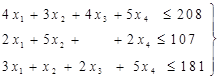(9)

где по смыслу задачи

x₁ ³ 0, x₂ ³ 0, x₃ ³ 0, x₄ ³ 0. (10)

Получили задачу на условный экстремум. Для ее решения систему неравенств (9) при помощи дополнительных неотрицательных неизвестных х₅ , х₆ , х₇ заменим системой линейных алгебраических уравнений

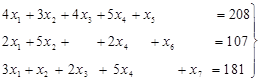(11)

где дополнительные переменные имеют смысл остатков соответствующих ресурсов. Среди всех решений системы уравнений (11), удовлетворяющих условию неотрицательности

х₁ ³0, х₂ ³0, … , х₅ ³0, … , х₇ ³0. (12)

надо найти то решение, при котором функция (8) примет наибольшее значение.

Воспользуемся тем, что правые части всех уравнений системы (11) неотрицательны, а сама система имеет предпочитаемый вид – дополнительные переменные являются базисными. Приравняв к нулю свободные переменные х₁ , х₂ , х₃ , х₄ , получаем базисное неотрицательное решение

11

x₁ =0, x₂ =0, x₃ =0, x₄ =0, x₅ =208, x₆ =107, x₇ =181 (13)

первые четыре компоненты которого определяют производственную программу

x₁ =0, x₂ =0, x₃ =0, x₄ =0 (14)

по которой мы пока ничего не производим.

Из выражения (8) видно, что наиболее выгодно начинать производить продукцию четвертого вида, так как прибыль на единицу продукции здесь наибольшая. Чем больше выпуск в этой продукции, тем больше прибыль. Выясним, до каких пор наши ресурсы позволяют увеличить выпуск этой продукции. Для этого придется записать для системы уравнений (11) общее решение

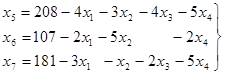(15)

Мы пока сохраняем в общем решении х₁ =х₂ =х₃ =0и увеличиваем только х₄ . При этом значения базисных переменных должны оставаться неотрицательными, что приводит к системе неравенств

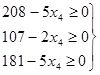или 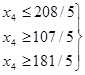т.е. 0 £ х₄ £

Дадим х₄ наибольшее значение х₄ =181/5, которое она может принять при нулевых значениях других свободных неизвестных, и подставим его в (15). Получаем для системы уравнений (11) частное неотрицательное решение

х₁ =0, х₂ =0, х₃ =0, х₄ =; x₅ =27; x₆ =; x₇ =0 (16)

Нетрудно убедиться, что это решение является новым базисным неотрицательным решением системы линейных алгебраических уравнений (11), для получения которого достаточно было принять в системе (11) неизвестную х₄ за разрешающую и перейти к новому предпочитаемому виду этой системы, сохранив правые части уравнений неотрицательными, для чего за разрешающее уравнение мы обязаны принять третье, так как

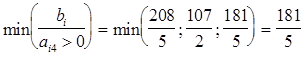
а разрешающим элементом будет а₃₄ =5. Применив известные формулы исключения, получаем для системы уравнений (11) новый предпочитаемый эквивалент

x₁ + 2x₂ + 2x₃ + x₅ - x₇ = 27

x₁ + x₂ - x₃ + x₆ - x₇ = (17)

x₁ + x₂ + x₃ + x₄ + x₇ =

Приравняв к нулю свободные переменные х₁ , х₂ , х₃ , х₇ , получаем базисное неотрицательное решение, совпадающее с (16), причем первые четыре компоненты его определяют новую производственную программу

х₁ =0, х₂ =0, х₃ =0, х₄ =. (18)

12

?????????, ???????? ?? ??? ????????? ?????????, ?.?. ???????????? ?? ??? ?????????? ???????. ??? ????? ??????? ??????? ??????? (8) ????? ????? ????????? ?????????? ?₁ , ?₂ , ?₃ , ?₇ .

Из последнего уравнения системы (17) выражаем базисную переменную х₄ через свободные и подставляем в (8). Получаем

(19)

Видим, что программа (18) не является наилучшей, так как прибыль будет расти, если мы начнем производить или первую, или вторую, или третью продукцию, но наиболее быстро функция z растет при возрастании х₁ . Поэтому принимаем х₁ в системе (17) за разрешающую неизвестную, находим разрешающее уравнение по