Реферат: Рассеяние рентгеновских лучей на молекулах фуллерена

Наиболее простой разновидностью колебаний являются гармонические. Координата материальной точки с течением времени при гармонических колебаниях изменяется по закону

x(t) =Acos(wt + j0) (1.3)

где A – амплитуда смещения (максимальное смещение точки от положения равновесия), w – частота, связанная с периодом соотношением

w = 2p / T. (1.4)

Положением равновесия называется месторасположение материальной точки, в котором сумма действующих на нее сил равна нулю.

Аргумент косинуса wt + j0 в функции (1.3) называется фазой колебания. Видно, что фаза является безразмерной величиной и линейной функцией времени. Постоянная величина j0 называется начальной фазой.

Колебания физических систем, приведенных на рис.1.1. – 1.6. совершали бы строго гармонические колебания при следующих дополнительных условиях:

Система 1.1. – при отсутствии сопротивления воздуха, система 1.2. – при отсутствии терния, система 1.3. – при малых углах и отсутствии сопротивления воздуха, системы 1.4. и 1.5. – при отсутствии вязкости жидкости, система 1.6. – при отсутствии активного сопротивления катушки и проводов.

Рассмотрим для простоты сначала одномерные гармонические колебания, когда материальная точка смещается вдоль одной прямой.

Вычислив производную функции (1.3) по времени получим скорость материальной точки:

v(t) = -wAsin(wt+j0) (1.5)

Видно, что скорость является также периодической функцией времени.

Теперь возьмем производную от функции (1.5) по времени и получим ускорение материальной точки.

a(t) = -w2 Acos(wt+j0) (1.6)

Сравнивая функции (1.3) и (1.6) получим что координата и ускорение связанны следующим выражением

a(t) = -w2 x(t),(1.7)

которое выполняется в любой момент времени.

Иначе говоря, при любых одномерных гармонических колебаниях ускорение частицы прямо пропорционально её координате, причем коэффициент пропорциональности отрицательный.

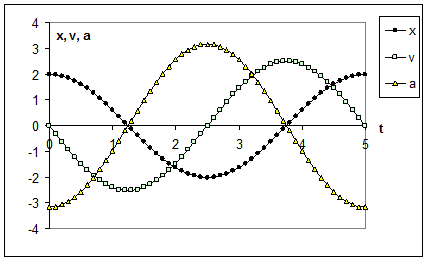
Рис.1.7. Зависимости от времени координаты (кружочки), скорости (квадратики) и ускорения (треугольники) частицы, совершающей одномерные гармонические колебания. Амплитуды А=2, период Т=5, начальная фаза j0=0.

Как известно, ускорение частицы (по основному закону динамики) прямо пропорционально силе, действующей на частицу. Следовательно, если сила прямо пропорциональна координате с обратным знаком, то частица будет совершать гармоническое колебание. Такие силы называются возвращающими.

Важным примером возвращающей силы является сила Гука (упругая сила). Таким образом, если на материальную точку действует сила Гука, то точка совершает гармонические колебания.

Так как мы рассматриваем одномерные колебания, то для анализа задачи достаточно спроецировать вектор силы Гука на ось, параллельную этой силе. Если ноль отсчета координаты x выбран в точке, в которой возвращающая сила равна нулю, то проекция силы равна

Fx = -kx,(1.8)

где коэффициент k называется жесткостью.

Сравнивая уравнения (1.7) и (1.8), и используя 2-й закон Ньютона, получим важное выражение для частоты колебаний:

w2 = k / m(1.9)

Это означает, что частота колебаний описывается параметрами физической системы, а не зависит от начальных условий. В частности, выражение (1.9) определяет частоту гармонических колебаний систем, показанных на рис.1.1. и 1.2.

В качестве поучительно примера рассмотрим одномерные движения, которые совершают грузы, прикрепленные к пружинам (см. рис.1.8).