Реферат: Рассеяние рентгеновских лучей на молекулах фуллерена

d0 =Acos(j0) (1.18)

0 = -wAsin(j0) (1. 19)

Решением системы (1.18) – (1. 19) являются следующие значения A = d0 и j0= 0.

Для других начальных условий величины A и j0, естественно приобретут другие значения.

Теперь рассмотрим систему, изображенную на рис.1.8. б. На груз в этом случае действуют только две силы: сила тяжести mg и сила упругости F (см. рис.1.10). Ясно, что в положении равновесия эти силы компенсируют друг друга, следовательно, пружина растянута.

Пусть груз несколько смещается по вертикали. Тогда векторное уравнение движение будет иметь вид, аналогичный уравнению (1.12)

ma = mg – kd(1. 20)

причем независимо от направления вертикального смещения (вверх или вниз).

Все векторы в уравнении (1. 20) направлены вертикально, поэтому это уравнение целесообразно спроецировать на вертикальную ось координат. Направим ось вниз, а начало координат выберем в точке, где тело находится в состоянии равновесия (см. рис.1.10).

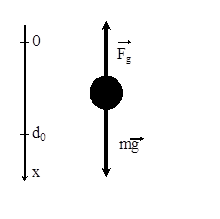
Рис.1.10. Силы, действующие груз, висящий на пружине.

Спроецировав (1.18) на ось X получим:

a = g – (k/m) d(1.21)

где a – проекция ускорения тела, d – проекция деформации пружины.

Для решения уравнения (1.21) полезно вернуться к положению равновесия груза. Уравнение Ньютона для этого положения имеет вид:

0 = g – (k/m) d0(1.22)

где d0 –деформации пружины при равновесии груза. Следовательно, вектор d0 равен

d0 = mg/k(1.23)

Видно, что в положении равновесия тела пружина действительно растянута, так как вектор d0 направлен параллельно вектору g, т.е. вниз.

Теперь поместим начало координат в точке равновесия груза на пружине, и тогда уравнение (1.21) примет вид:

a = g – (k/m) (x+ d0) (1.24)

где d0 –модуль вектора деформации пружины d0.

Подставив в уравнение (1.24) величину d0, полученную из соотношения (1.23), получим:

a = g – (k/m) (x+ (m/k) g)

или

a = – (k/m) x (1.25)

Полученное уравнение полностью совпадает с уравнением (1.16). Таким образом, тело, изображенное на рис.1.8. б, совершает также гармоническое колебательное движение, описываемое функцией (1.3), как и груз в системе, изображенной на рис.1.8. а. Частота колебаний Отличие заключается лишь в направлении колебаний (вертикальное вместо горизонтального). Но частота колебаний по-прежнему определяется жесткостью пружины и массой груза формулой (1.9).

Характерно, что начальная деформация пружины в системе на рис.1.8. б не влияет на частоту колебаний.

2.1.3. Сложение колебаний

2.1.3.1. Сложение двух гармонических колебаний с одинаковыми амплитудами и частотами

Рассмотрим пример звуковых волн, когда два источника создают волны с одинаковой амплитудами A и частотами ω. На расстоянии от источников установим чувствительную мембрану. Когда волна «пройдёт» расстояние от источника до мембраны, мембрана придёт в колебательное движение. Воздействие каждой из волн на мембрану можно описать следующими соотношениями, воспользовавшись колебательными функциями: