Реферат: Рассеяние рентгеновских лучей на молекулах фуллерена

Рис.1.8. Грузы на пружинах.

Пусть массы пружин пренебрежимо малы по сравнению с массами грузов.

Грузы рассматриваются как материальные точки.

Сначала рассмотрим систему, изображенную на рис.18. а. Предположим, что первоначально груз был смещен влево и, как следствие пружина растянулась. При этом на груз (материальную точку) действуют 3 силы: сила тяжести mg, сила упругости F и сила нормальной реакции опоры N. Трением в данной задаче мы пренебрегаем (см. рис.1.9).

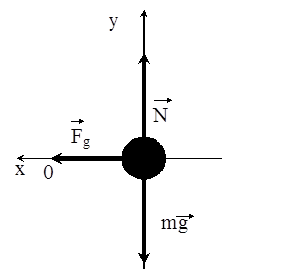
Рис.1.9. Силы на груз, лежащий на гладкой опоре, при растяжении пружины.

Запишем второй закон Ньютона для тела, изображенного на рис.1.9.

ma = mg + F + N(1.10)

Сила упругости при небольших деформациях пружин описывается законом Гука

F = – kd(1.11)

где d – вектор деформации пружины, k – коэффициент жёсткости пружины.

Заметим, что при движении груза растяжение пружины может сменяться сжатием. При этом вектор деформации d будет менять свое направление на противоположное, следовательно, то же будет происходить с силой Гука (1.11). Из этого, в частности, следует, что при начальном сжатии пружины векторное уравнение движение (1.10) будет иметь тот же вид:

ma = mg – kd + N(1.12)

Выберем начало координат в точке расположения груза при недеформированной пружине. Ось X направим горизонтально, ось Y –вертикально, т.е. перпендикулярно опоре (см. рис.1.9).

Так как груз движется вдоль опоры по горизонтали, то проекция ускорения на ось Y равна нулю. Тогда сила тяжести полностью компенсируется нормальной реакции опоры

N + mg = 0 (1.13)

Проецирование уравнения движения (1.12) на ось X дает скалярное уравнение:

ma = – kd,(1.14)

где a – горизонтальная проекция ускорения груза, d – проекция вектора деформации пружины.

Иначе говоря, ускорение направлено по горизонтальной оси X и равно

a = – (k/m) d(1.15)

Еще раз заметим, что уравнение (1.15) справедливо и при растяжении, и при сжатии пружины.

Так как начало координат выбрано так, что оно совпадает с концом недеформированной пружины, то проекция деформации совпадает со значением горизонтальной координаты груза x:

a = – (k/m) x (1.16)

По определению проекция ускорения равна второй производной соответствующей координаты по времени. Следовательно, одномерное уравнение движения (1.16) можно переписать в виде

(1.17)

Иначе говоря, проекция ускорения прямо пропорциональна координате, причем коэффициент пропорциональности имеет отрицательный знак.

Уравнение (1.17) является дифференциальным второго порядка, общая теория решения таких уравнений изучается в курсе математического анализа. Однако легко доказать непосредственной подстановкой, что функция гармонических колебаний (1.3) удовлетворяет уравнению (1.17). Как уже было доказано ранее, частота колебаний выражается формулой (1.9).

Амплитуда A и начальная фаза j0 колебаний определяются из начальных условий.