Реферат: Решение задач линейной оптимизации симплекс – методом

Пусть - оптимальный опорный план вспомогательной задачи. Тогда является опорным планом исходной задачи. Действительно, все дополнительные переменные . Значит, удовлетворяет условиям исходной задачи, т.е. является некоторым планом задачи (2.12) - (2.13). По построению план является также опорным.

3.1. Постановка L -задачи

Вспомогательная задача для нахождения начального опорного плана задачи (2.12) - (2.13) в канонической форме состоит в следующем.

Требуется обратить в максимум

при условиях

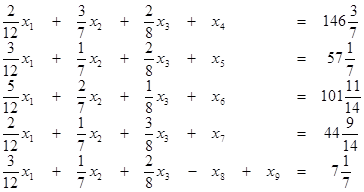
, где .

???????????? ? ???????? ????????? ???????? ????? ????

Здесь добавление только одной дополнительной переменной (вместо пяти) обусловлено тем, что исходная задача уже содержит четыре единичных вектора условий А _4, А _5, А _6, А _7.

3.2. Решение L -задачи

Решение L-задачи будем проводить в соответствии с первым алгоритмом симплекс-метода (описание алгоритма приводится в п.4). Составим таблицу, соответствующую исходному опорному плану (0-й итерации).

Т.к. Б ₀ = - базис, соответствующий известному опорному плану, является единичной матрицей, то коэффициенты разложения векторов А _j по базису Б ₀

.

Значение линейной формы и оценки для заполнения (m+1)-й строки таблицы определяются следующими соотношениями:

,

.

Отсюда получим:

;

;

;

…

.

Весь процесс решения задачи приведен в табл. 3.2.1, которая состоит из 2 частей, отвечающих 0-й (исходная таблица) и 1-й итерациям.

Заполняем таблицу 0-й итерации.

Среди оценок имеются отрицательные. Значит, исходный опорный план не является оптимальным. Перейдем к новому базису. В базис будет введен вектор А ₁ с наименьшей оценкой . Значения t вычисляютсядля всех позиций столбца t (т.к. все элементы разрешающего столбца положительны). Наименьший элемент достигается на пятой позиции базиса. Значит, пятая строка является разрешающей строкой, и вектор А ₉ подлежит исключению из базиса.

Составим таблицу, отвечающую первой итерации.

В столбце Б_х , в пятой позиции базиса место вектора А₉ занимает вектор А₁ . Соответствующий ему коэффициент линейной формы С₄₁ = 0 помещаем в столбец С_х . Главная часть таблицы 1 заполняется по данным таблицы 0 в соответствии с рекуррентными формулами. Так как все , то опорный план является решением L-задачи. Наибольшее значение линейной формы равно .

Таблица 3.2.1

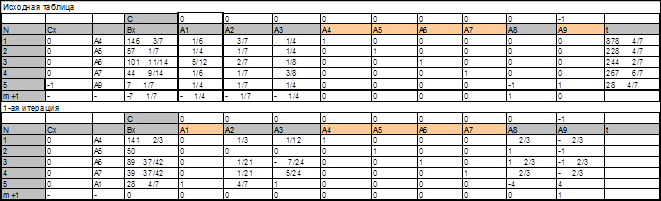
3.3. Формирование начального опорного плана исходной задачи линейного программирования из оптимального плана L -задачи