Реферат: Решение задач линейной оптимизации симплекс – методом
Оценки 
позволяют установить оптимальность рассматриваемого опорного плана и определить вектор Ак , вводимый в базис. Коэффициенты 
разложения вектора Ак по текущему базису вычисляются по формуле
.
Как и в I алгоритме, вектор, подлежащий исключению из базиса, определяется величиной
.
Таким образом при втором алгоритме на каждом шаге запоминаются базисные компоненты 
, обратная матрица 
, значение линейной формы F(X) и векторY , соответствующие текущему опорному плану Х . Элементы столбцов матрицы удобно рассматривать как коэффициенты 
разложения единичных векторов 
по векторам базиса. Рекуррентные формулы, связывающие параметры двух последовательных итераций
; (6.3)
. (6.3)
Здесь
.
Результаты вычислений сводятся в основные таблицы (вида табл. 6.1) и вспомогательную таблицу (вида табл. 6.2); столбцы В , е1 , …, еm основных таблиц (все m +1 позиций) называют главной частью этих таблиц. Столбец Аk – разрешающий столбец, строка l – разрешающая строка.
Таблица 6.1 Таблица 6.2
| N |  |  | B |  | … |  |  | t | N | B |  |  | … |  |
| 1 |  |  |  |  | … |  |  | 1 |  |  |  | … |  | |
 | | | | | | | | | | | | | | |
| l |  |  |  |  | … |  |  |  | m |  |  |  | … |  |
| | | | | | | | | m +1 | C |  |  | … |  |
| M |  |  |  |  | … |  |  | 0 |  |  |  | … |  | |
| m +1 | – | – |  |  | … |  |  | – | 1 |  |  |  | … |  |
| 2 |  |  |  | … |  | |||||||||
| … | … | … | … | … | … |
Краткое описание алгоритма.
1. Нулевая итерация:
а) составляется вспомогательная табл. 6.2, в которую вносятся параметры задачи; дополнительная строка таблицы с номером ν заполняется по мере выполнения ν -й итерации;
б) составляется основная табл. 6.1 с номером 0, в которой заполняются первые m строк, за исключением последних двух столбцов Аk и t. Элементы 
и 
определяются скалярными произведениями (Cx , ej ) и (Cx , B ) соответственно. Нулевая итерация заканчивается заполнением нулевой дополнительной строки вспомогательной таблицы с оценками 
.
2. (ν +1)-я итерация .
Пусть ν -я итерация закончена. В результате заполнена ν -я основная таблица, за исключением двух последних столбцов, и ν -я дополнительная строка вспомогательной таблицы. Просматривается эта строка. Если все 
, то опорный план 
- решение задачи. Если хотя бы одна 
, то в базис вводится вектор А k с 
(обычно 
). После этого заполняется столбец 
основной таблицы. В позицию (m +1) этого столбца заносится оценка 
вектора Аk . Остальные элементы этого столбца равны
.
Возможны два случая:
1) все 
- задача неразрешима;
2) 
хотя бы для одного i . В этом случае, также как и в первом алгоритме, заполняется столбец (t ) основной таблицы ν , определяется разрешающий элемент 
. Главная часть заполняется по рекуррентной формуле (6.3). Заполняется (ν +1)-я дополнительная строка вспомогательной таблицы. На этом заканчивается (ν +1)-я итерация.
Решение М-задачи
Таблица 6.3
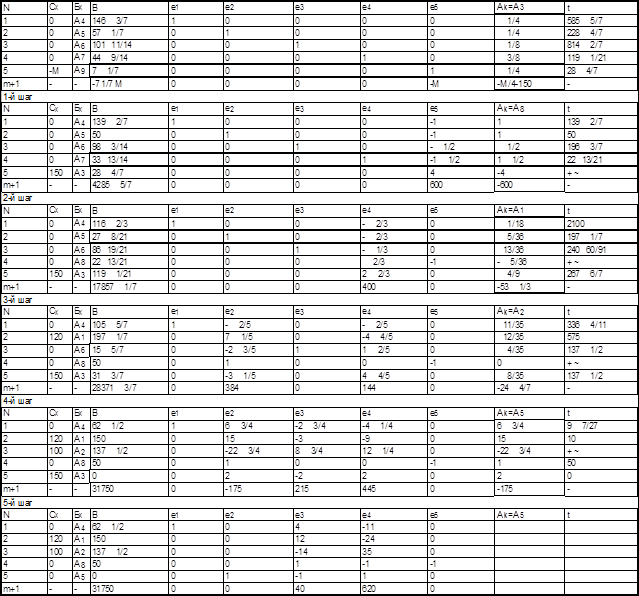
Таблица 6.4
Задача (5.4), (5.5) имеет опорный план Х0 = (0, 0, 0,