Реферат: Решение задач линейной оптимизации симплекс – методом

4. Решение исходной задачи I алгоритмом симплекс-метода

Описание I алгоритма

Симплекс-метод позволяет, отправляясь от некоторого исходного опорного плана и постепенно улучшая его, получить через конечное число итераций оптимальный план или убедиться в неразрешимости задачи. Каждой итерации соответствует переход от одной таблицы алгоритма к следующей. Таблица, отвечающая опорному плану в ν -й итерации имеет вид табл. 4.1.

Таблица 4.1

C		…		…		…
N			B		…		…		…		t
1					…		…		…
l					…		…		…
m					…		…		…
m +1	–	–			…		…		…		–

Заполнение таблицы, соответствующей исходному опорному плану (0-й итерации) . Пусть некоторый опорный план задачи (2.1) - (2.3) с базисом . Тогда – базисные компоненты, а – небазисные компоненты.

Вычисляем коэффициенты разложения векторов А_j по базису Б₀

(в случае, если Б₀ является единичной матрицей, )

и находим оценки . Далее определяем значение линейной формы

Полученные результаты записываем в таблицу 4.1.

В первом столбце N таблицы указываются номера строк. Номера первых m строк совпадают с номерами позиций базиса. Во втором столбце С_х записываются коэффициенты линейной формы при базисных переменных. Столбец Б_х содержит векторы базиса . В столбце В записываются базисные переменные опорного плана. Столбцы содержат коэффициенты разложения соответствующих векторов условий по векторам базиса. Все вышесказанное относится только к первым m строкам таблицы. Последняя (m +1)-я строка таблицы заполняется последовательно значением линейной формы F и оценками . Позиции таблицы, которые не должны заполняться, прочеркиваются.

В результате заполнена таблица 0-й итерации кроме столбца t .

Столбцы В , А₁ ,…, A_n (все m +1 позиций) будем называть главной частью таблицы.

Порядок вычислений в отдельной итерации . Пусть ν -я итерация закончена. В результате заполнена таблица ν за исключением последнего столбца t .

Каждая итерация состоит из двух этапов.

I этап: проверка исследуемого опорного плана на оптимальность.

Просматривается (m +1)-я строка таблицы ν . Если все , то опорный план, полученный после ν -й итерации, является оптимальным (случай 1), завершаем решение задачи. Пусть теперь имеются отрицательные оценки. Проверяем знаки элементов столбцов с . Наличие по крайней мере одного столбца , для которого и все , свидетельствует о неразрешимости задачи (случай 2). Установив это, прекращаем вычисления.

Если в каждом столбце , для которого , содержится хотя бы один положительный коэффициент , то опорный план является неоптимальным (случай 3). Переходим ко II этапу.

II этап: построение нового опорного плана с большим значением линейной формы.

Определяется векторA_k , который должен быть введен в базис, из следующего условия

.

После этого заполняется последний столбец таблицы ν – столбец t . В него записываются отношения базисных переменных (элементы столбца В) к соответствующим составляющим (элементы столбца A_k ). Т.о. заполняются только те позиции, для которых . Если , то в позиции i столбца t записывается . Вектор базиса , на котором достигается t₀ ,

,

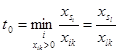подлежит исключению из базиса (если t₀ достигается на нескольких векторах, то из базиса исключается любой из них).

Столбец A_k , отвечающий вектору, вводимому в базис, и l -я строка, соответствующая вектору , исключаемому из базиса, называется соответственно разрешающим столбцом и разрешающей строкой . Элемент , расположенный на пересечении разрешающего столбца и разрешающей строки, называется разрешающим элементом .

После выделения разрешающего элемента заполняется (ν +1)-я таблица. В l -е позиции столбцов Б_х , С_х вносятся соответственно А_к , С_к , которые в (ν +1)-й таблице обозначаются как , . В остальные позиции столбцов Б_х , С_х вносятся те же параметры, что и в таблице ν .

Далее заполняется главная часть (ν +1)-й таблицы. Прежде всего происходит заполнение ее l- й строки в соответствии с рекуррентной формулой

.

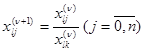Рекуррентная формула для заполнения i -й строки (ν +1)-й таблицы имеет вид