Реферат: Ряды Фурье и их приложения

Оценка коэффициентов Фурье. (Бугров)

Теорема 1. Пусть функция ƒ(x) периода 2π имеет непрерывную производную ƒ^{( s)} (x) порядка s, удовлетворяющей на всей действительной оси неравенству:

│ ƒ^{( s)} (x)│≤ M_s ; (5)

тогда коэффициенты Фурье функции ƒ удовлетворяют неравенству

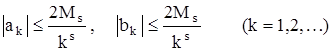(6)

Доказательство. Интегрируя по частям и учитывая, что

ƒ(-π) = ƒ(π), имеем

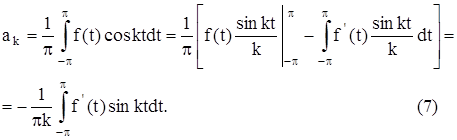
Поэтому

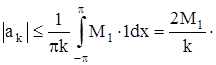
Интегрируя правую часть (7) последовательно, учитывая, что производные ƒ^΄ , …, ƒ^{( s-1)} непрерывны и принимают одинаковые значения в точках t = -π и t = π, а также оценку (5), получим первую оценку (6).

Вторая оценка (6) получается подобным образом.

Теорема 2. Для коэффициентов Фурье ƒ(x) имеет место неравенство

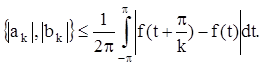(8)

Доказательство. Имеем

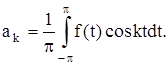(9)

Вводя в данном случае замену переменной и учитывая, что ƒ(x) – периодическая функция, получим

Складывая (9) и (10), получаем

Отсюда

Аналогичным образом проводим доказательство для b_k .

Следствие. Если функция ƒ(x) непрерывна, то её коэффициенты Фурье стремятся к нулю: a_k → 0, b_k → 0, k → ∞.

Пространство функций со скалярным произведением.

Функция ƒ(x) называется кусочно-непрерывной на отрезке [a, b], если она непрерывна на этом отрезке, за исключением, может быть, конечного числа точек, где она имеет разрывы первого рода. Такие точки можно складывать и умножать на действительные числа и получать как результат снова кусочно-непрерывные на отрезке [a, b] функции.

Скалярным произведением двух кусочно-непрерывных на [a, b] (a < b) функций ƒ и φ будем называть интеграл

(11)

Очевидно для любых кусочно-непрерывных на [a, b] функций ƒ , φ , ψ выполняются свойства: