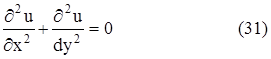Реферат: Ряды Фурье и их приложения
Полагая ещё 
получим для частичных сумм ряда Фурье выражение
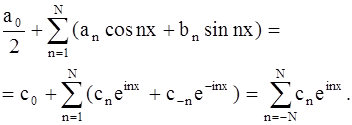
Для новых коэффициентов cn получаем формулу (учитывая формулы an и bn ).
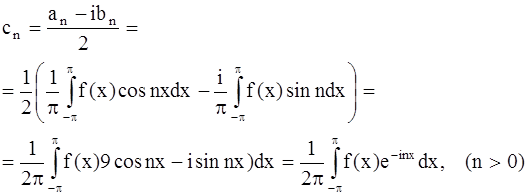
Непосредственно видно, что эта формула верна для n = 0 и для n < 0 (последнее видно, например, из того, что 
где 
обозначает число, сопряженное с).
По доказанному имеем в точках дифферуемциемоcти:
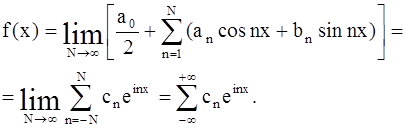
Итак, в точках дифференцируемости
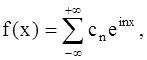(26)
где
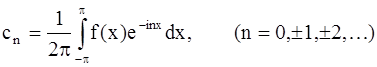
Правая часть формулы (26) представляет собой комплексную форму ряда Фурье для функции с периодом 2π.
Комплексная форма ряда Фурье для функции с любым периодом. (Романовский стр.33)
Пусть ƒ(x) – функция с периодом 2l , удовлетворяющая условиям , указанным в пункте 6. Тогда подстановка x= l t/ π приводит нас к функции ƒ(l t/ π) с периодом 2π. В силу предыдущего пункта в точках дифференцируемости имеем:
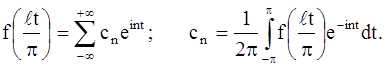
Переходя как в ряде, так и формулах для коэффициентов к старому переменному х и замечая, что t = π x / l , dt=(π / l )dx, получим в точках дифференцируемости:
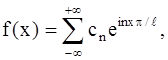(27)
где
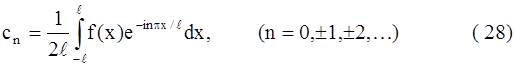Правая часть формулы (27), где коэффициенты определяются равенствами (28), называется комплексной формой ряда Фурье для функции с периодом 2l .
Основные типы уравнений математической физики.
Основными уравнениями математической физики называют (для случая функций двух независимых переменных) следующие дифференциальные уравнения с частными производными второго порядка.
1. Волновое уравнение:
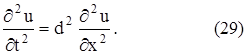
К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т. д. Это уравнение является простейшим уравнением гиперболического типа.
2. Уравнение теплопроводности или уравнение Фурье:
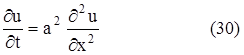
К исследованию этого уравнения приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде (например, фильтрации нефти и газа с подземных песчаниках), некоторые вопросы теории вероятностей и т. д. Это уравнение является простейшим уравнением параболического типа.
3. Уравнение Лапласа:
