Реферат: Ряды Фурье и их приложения
Обратим внимание, что постоянная ![]() в (2) пишется в таком виде, чтобы придать единообразие формулам (17) и (18).
в (2) пишется в таком виде, чтобы придать единообразие формулам (17) и (18).
Вышеприведенные соображения показывают, что поиски тригонометрического разложения данной функции целесообразно начать с изучения её ряда Фурье, откладывая на потом строгое изучение вопроса о том, для каких функций ряд сходится, и притом именно к данной функции. Пока же этого не сделано, функции ƒ(x) сопоставляют её формальный ряд Фурье, что обычно записывают в виде:
![]() ƒ(x) ~
ƒ(x) ~ 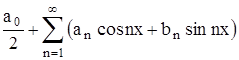 , (19)
, (19)
про который известно, что его коэффициенты вычислены по функции ƒ(x) по формулам Эйлера – Фурье (4), (17) и (18), но ничего не утверждается о его сходимости и тем более – о его сходимости к данной функции.
Из определения ряда Фурье не следует, что функция должна в него разлагаться. Из сказанного выше следует только, что некоторая функция допускает разложение в равномерно сходящийся ряд вида (19), то этот ряд будет её рядом Фурье.
3. Признаки сходимости ![]() рядов Фурье. (стр. 331, Пискунов)
рядов Фурье. (стр. 331, Пискунов)
Зададим вопрос: какими свойствами должна обладать функция, чтобы построенный, для неё ряд Фурье сходился и чтобы сумма построенного ряда Фурье равнялась значениям данной функции в соответствующих точках?
Сформулируем теорему, которая даст достаточные условия представимости функции ƒ(x) рядом Фурье. (из Пискунова)
Определение. Функция ƒ(x) называется кусочно- монотонной на отрезке [a, b], если этот отрезок можно разбить конечным числом точек х1 , х2 , …,хn-1 на интервалы (а, х1 ), (х1 , х2 ),…, (хn-1 , b) так, что на каждом из интервалов функция монотонна, т. е. либо не возрастающая, либо неубывающая.
Теорема.
Если периодическая функция ƒ(x) с периодом 2π – кусочно монотонная и ограниченная на отрезке [-π, π], то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда s(x) равна значению функции ƒ(x) в точках непрерывности функции. В точках разрыва функции ƒ(x) сумма ряда равняется среднему арифметическому пределов функции ƒ(x)справа и слева, т. е. если х = с – точка разрыва функции ƒ(x), то
![]() .
.
Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных отделах математики. Особенно успешно ряды Фурье применяются в математической физике и её приложениях к конкретным задачам механики и физики.
Этот вопрос можно решить с помощью теоремы Дирихле. («Краткий курс высшей математики», Шнейдер и др., стр. 181)
При выводе формул (4), (17), (18) мы заранее предполагали, что функция ƒ(x) разлагается в правильно сходящийся тригонометрический ряд (1). Если же такого предположения не делать, а допустить, что для функции ƒ(x) существуют все интервалы, стоящие в правых частях формул (4), (17), (18), то по этим формулам можно вычислить коэффициенты a0, ak и bk и составить тригонометрический ряд (1), который представляет собой ряд Фурье, соответствующий данной функции.
Является ли построенный таким образом ряд Фурье сходящимся и если он сходится, то имеем ли мы право утверждать, что он сходится именно к функции ƒ(x), с помощью которой вычислялись коэффициенты ряда?
Оказывается, что сходимость ряда Фурье к заданной функции имеет место для довольно широкого класса функций. Достаточные условия сходимости ряда Фурье, и, следовательно, возможность разложения функций в ряд Фурье даются теоремой Дирихле. Прежде чем формулировать эту теорему, введем два определения.
Функция ƒ(x) называется кусочно-монотонной на сегменте [a, b], если этот сегмент можно разделить на конечное число сегментов, внутри каждого, из которых функция либо только возрастает, либо только убывает, либо постоянна.
Основное определение. Функция ƒ(x) называется удовлетворяющей условиям Дирихле на сегменте [ a, b], если:
1)функция непрерывна на сегменте [ a, b] или же имеет
на нем конечное число точек разрыва 1 рода;
2) функция кусочно-монотонна на сегменте [ a, b].
3.1. Примеры разложения функций в ряды Фурье.
Пример 1. Периодическая функция ƒ(x) с периодом 2π определяется следующим образом: ƒ(x) = х , -π < x ≤ π.
Эта функция – кусочно монотонная и ограниченная. Следовательно, её можно разложить в ряд Фурье.
 |
По формуле (4) находим:

Применяя формулам (17), (18) и интегрируя по частям, получим:
