Реферат: Шар и сфера

Оглавление:

1. Вступление…………………………………………………………………………………..2

2. Шар и сфера…………………………………………………………………………………3

   1. Шар и шаровая поверхность……………………………………………………...3

   2. Взаимное расположение шара и плоскости……………………………………..3

   3. Принцип Кавальери. Нахождение объёмов тел с помощью принципа Кавальери…………………………………………………………………………..6

   4. Интегральное исчисление. Понятие интеграла…………………………………9

   5. Вычисление объёмов тел с помощью интеграла………………………………10

   6. Объём шара………………………………………………………………………12

   7. Шаровой сегмент. Объём шарового сегмента…………………………………12

   8. Шаровой слой. Объём шарового слоя…………………………………………14

   9. Шаровой сектор. Объём шарового сектора……………………………………14

   10. Площадь поверхности шара…………………………………………………17

   11. Площадь поверхности сектора шара……………………………………….18

   12. Площадь поверхности шарового пояса…………………………………….18

3.Задачи………………………………………………………………………………………20

3.1 Задачи на поверхности…………………………………………………………..20

3.2 Задачи на объёмы тел……………………………………………………………23

4.Заключение…………………………………………………………………………………25

5.Литература………………………………………………………………………………....26

2. Шар и сфера.

2.1. Шар и шаровая поверхность.

Ш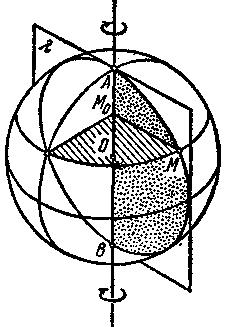аровой или сферической поверхностью называется геометрическое место точек пространст­ва, удаленных от данной точки О (центра) на заданное расстоя­ние R (радиус). Все пространство по отношению к данной ша­ровой поверхности разбивается на внут­реннюю область (куда можно присоеди­нить и точки самой поверхности) и внешнюю. Первая из этих областей назы­вается шаром. Итак, шар — геометрическое место всех точек, удаленных от заданной точки О (центра) на расстоя­ние, не превышающее данной величины R (радиуса). Шаровая поверхность яв­ляется границей, отделяющей шар от ок­ружающего пространства.

Шаровую поверхность и шар можно получить также, вращая окружность (круг) вокруг одного из диаметров.

Рассмотрим окружность с центром О и радиусом R (рис. 1), лежащую в плоско­сти Я. Будем вращать ее вокруг диаметра АВ. Тогда каждая из точек окружности, например М, в свою оче­редь опишет при вращении окружность, имеющую своим центром точку М₀—проекцию вращающейся точки М на ось враще­ния АВ. Плоскость этой окружности перпендикулярна к оси вращения. Радиус ОМ, ведущий из центра исходной окружности в точку М, будет сохранять свою величину во все время вра­щения, и потому точка М все время будет находиться на сфе­рической поверхности с центром О и радиусом R. Шаровая поверхность может быть получена вращением окружности вокруг любого из ее диаметров.

Сам шар как тело получается вращением круга; ясно, что для получения всего шара достаточно вращать полукруг около ограничивающего его диаметра.

2.2. Взаимное расположение шара и плоскости.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--