Реферат: Шар и сфера

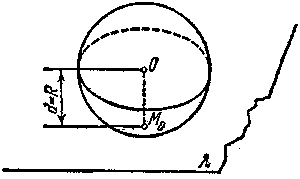поверхностью; такая плоскость называется касательной к шару. Радиус, проведенный в точку касания, перпендикулярен к касательной плоскости.

Д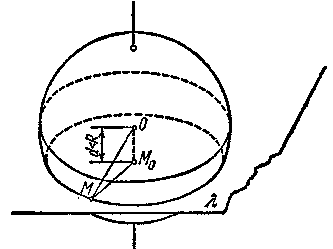ействительно, если плоскость имеет с поверхностью шара един­ственную общую течку, то эта точка ближайшая к центру шара по сравнению с остальными точ­ками плоскости и потому служит основанием перпендикуляра, опущенного из центра шара на плоскость.

Если, наконец, основание пер­пендикуляра М₀ окажется внут­ри шара (рис. 4), то плоскость будет пересекать поверхность шара, так как часть ее окажется внутри шара, а часть — вне. Исследуем линию пересечения такой плоскости с шаровой поверх­ностью. Пусть расстояние ее от центра шара равно d, d<R. Тогда оказывается, что линия пересечения плоскости с поверх­ностью шара является окружностью с центром в точке М₀ и радиусом, равным . Для доказательства проведем через М₀ произвольный луч М₀М, лежащий в секущей пло­скости. Выходя из внутренней области шара во внешнюю, он пересечет поверхность шара в некоторой точке М. Рассмотрим треугольник ОМ₀М с прямым углом при вершине М₀. Катет М₀М по теореме Пифагора будет равен . Впрочем, постоянство длины отрезка независимо от направления луча М₀М в данной плоскости видно и без применения теоремы Пифагора (пользуемся равенством прямоугольных треугольников, имеющих общие катеты и равные гипотенузы). Теперь видно, что все точ­ки пересечения плоскости , с поверхностью шара лежат на од­ной окружности с центром М₀ и радиусом, равным. Напротив, любая точка этой окружности удалена от центра шара на расстояние, равное , и потому лежит на поверхности шара (равно как и в плоскости ) и, значит, принадлежит рассматриваемой линии пересечения. Из этого видно, что линия пересечения - полная окружность, а не какая-либо часть ее.

Итак, если длина перпендикуляра, опущенного из центра О шара радиуса R на данную плоскость, равна d, то:

1. при d>R плоскость не пересекает шара;

2. при d = R плоскость касается шара в одной точке, радиус,
   проведенный в точку касания, перпендикулярен к плоскости;

3. при d<R плоскость пересекает шар по окружности, цент­
   ром которой служит основание перпендикуляра, опущенного из

центра шара на плоскость, а радиус равен.

В частности, плоскость, проходящая через центр шара, пере­секает его по окружности максимально возможного радиуса, равного радиусу шара R. Такие сечения шара плоскостями, про­ходящими через его центр, называются большими кругами шара.

Для наглядности вышеизложенного материала я предлагаю решить две небольшие задачи.

Задача 1. Два сечения шара радиуса 10 см параллельны­ми плоскостями имеют радиусы, равные 6 еж и 8 см. Найти расстояние между секущими плоскостями.

Решение. Находим расстояние каждой из параллельных плоскостей до центра шара:

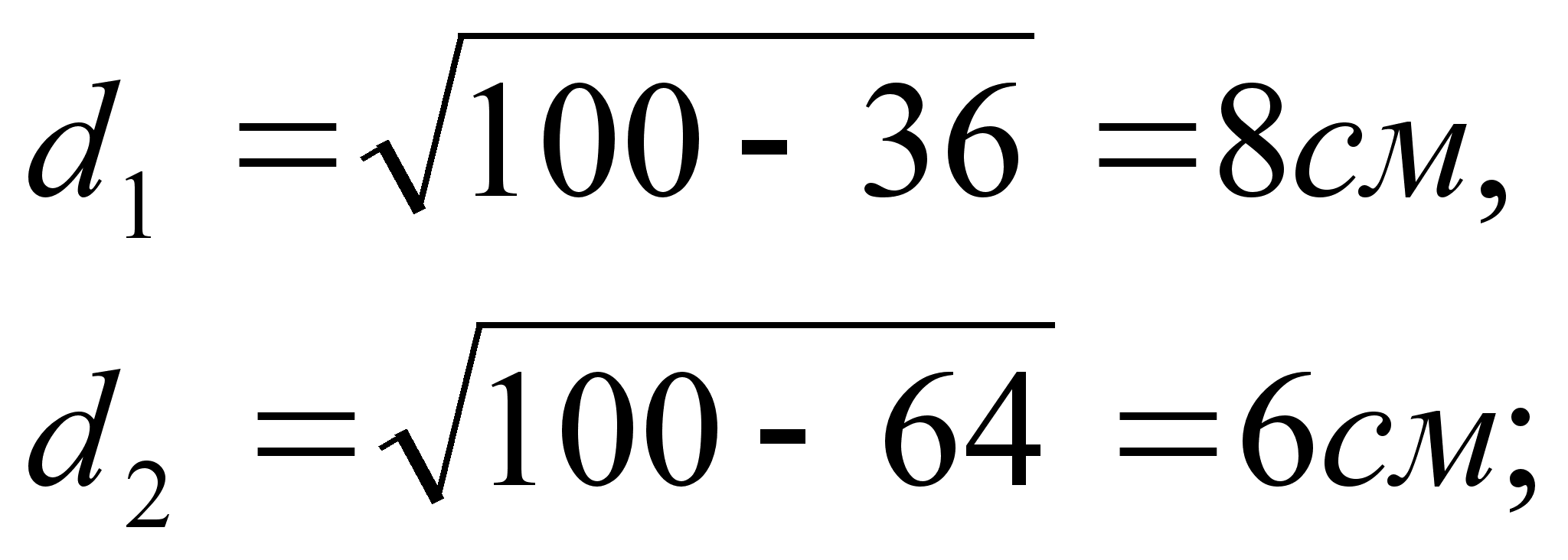
в зависимости от того, лежит ли центр шара между плоскостями или нет, получаем два различных ответа к задаче:

Задача 2. Расстояние между центрами двух шаров равно d; радиусы их R₁ и R₂. Найти радиус окружности, по которой они пересекаются.

Р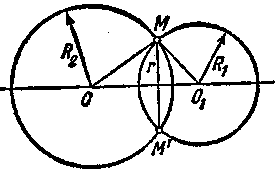ешение. Искомый радиус служит высотой треугольника OMO₁ (рис. 5). Площадь S треугольника ОМО₂ находится по трем сторонам 00₁ = d, R₁ R₂ и искомый радиус равен r=2S/d. Прямая линия также может занимать по отношению к шару три существенно различных положения. Именно, она может пе­ресечь поверхность шара в двух различных точках, не пересе­кать ее или иметь с ней одну общую точку. В последнем слу­чае она будет называться касатель­ной к шару.

2.3. Принцип Кавальери. Нахождение объёма шара с помощью принципа Кавальери.

В Европе XVII-ХVIII веков и, прежде всего, в экономически развитых государствах, укреплялся новый общественный строй - капитализм. Составной частью этого процесса была техническая революция - переход от мануфактурной промышленности к фабричной и, как следствие, серия изобретений, среди которых - создание паровой машины. Стремительное развитие математики в эту эпоху было обусловлено также усовершенствованием машин для предприятий, изобретением огнестрельного оружия и книгопечатания, постройкой судов для океанского плавания. Возникла необходимость теоретического и научного изучения движения, изменения вообще.

Открытия в астрономии, связанные с именами Н. Коперника и И. Кеплера, позволили по-новому взглянуть на место человека во Вселенной и его умение рациональным образом объяснить астрономические явления. Законы небесной механики дали возможность дополнить законы Земли.

И. Кеплер практически всю свою жизнь посвятил изучению, развитию и пропаганде гелиоцентрической системы Коперника. Анализируя огромный материал астрономических наблюдений, он в 1609-1619 гг. открыл три закона движения планет, носящие его имя, среди которых закон, связанный с площадью сектора.

Задача вычисления секториальных площадей требовала умения пользоваться бесконечно малыми величинами. Этих знаний недоставало и для решения других задач практического характера. Круг, в представлении Кеплера, состоял из бесконечно большого числа треугольников с общей вершиной в центре, а шар - из бесконечно большого числа утончающихся пирамид с вершинами в его центре. Книга ученого «Стереометрия винных бочек» (1615 г.) произвела большое впечатление на читателей, так как в ней был описан доступный метод определения объема 93 различных тел вращения (бочек). Каждому из них он дал оригинальное название: лимон, груша, чалма и т. п. Кеплер заменял неизвестный объем известным путем деления данного тела на сколь угодно малые части и образования из них нового тела (быть может, путем деформации), объем которого можно найти. Доказательства были нестрогими, и это вызывало много споров у математиков. Как видим, Кеплер получил новый результат весьма простым приемом. «Стереометрия винных бочек» - первая работа того времени, вводящая в геометрию бесконечно малые величины и принципы интегрального исчисления, хотя, как говорил сам ученый во введении к этой книге, поводом и целью написания труда первоначально явился частный и практический вопрос об измерении объема винных бочек с помощью одного промера их поперечной длины. Интерес математиков сосредотачивался главным образом на общих принципах определения объемов тел вращения с помощью бесконечно малых величин.

Среди таких математиков был итальянский монах Бонавентура Кавальери (1598-1647). Он занимал кафедру математики в Болонском университете. В переписке с астрономом и математиком Г. Галилеем они обсуждали разнообразные механические и математические проблемы, и в частности метод «неделимых». Галилей собирался, но так и не написал книгу об этом методе, зато у Кавальери в 1635 г. вышла книга «Геометрия, изложенная новым способом при помощи неделимых частей непрерывных величин». При вычислении площадей многоугольников бывает полезно преобразовывать фигуры, не меняя их площадей, например, разрезать на части и составлять новые (так называемые равносоставленные фигуры). Так можно преобразовать друг в друга треугольники с равными основаниями и высотами. Можно ли аналогичным образом преобразовывать криволинейные фигуры? Кавальери представляет их себе состоящими из бесконечно тонких параллельных плоских слоев - «неделимых» или «нитей» и утверждает, что площадь не меняется при сдвигах этих слоев друг относительно друга. Иначе, принцип Кавальери состоит в том, что если пересечь фигуру семейством всех прямых, параллельных заданной, то длины пересечений полностью определят площадь фигуры. В частности, если у двух фигур эти длины совпадают, то они равновелики. Строгого обоснования своего принципа Кавальери не дал, но рассмотрел его многочисленные применения. Например, на основе этого принципа легко получается равновеликость треугольников с равными основаниями и высотами.

Одно из самых удивительных применений принципа Кавальери принадлежит французскому математику Ж. Робервалю (1602-1675), который нашел площадь сегмента, ограниченного одной аркой циклоиды.

Еще более эффективен принцип Кавальери при нахождении объемов тел. Он состоит в том, что объем тела определяется площадями его пересечений «всеми плоскостями», параллельными некоторой заданной.

Однако интегральное исчисление содержит общие методы для вычисления площадей и объемов, причем там, где применение принципа Кавальери требовало нестандартных построений, к успеху приводят стандартные вычисления, и постепенно принцип Кавальери отошел в область истории. Но поскольку по принципу Кавальери легко вычисляются все «школьные» объемы и площади, неоднократно предлагалось принять принцип Кавальери в школьной геометрии за аксиому.

Видный советский ученый, историк математики, профессор Д. Д. Мордухай-Болтовский (1876—1952), которому принадле­жит самый совершенный русский перевод «Начал» Евклида с об­стоятельными комментариями, дал интересный вывод формулы объема шара на основе принципа Кавальери.

Вот это доказатель­ство.

П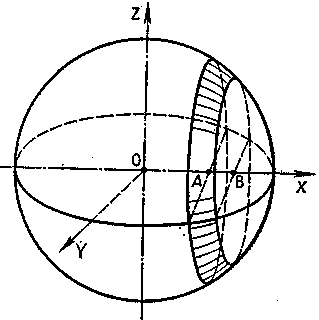оместим между двумя парал­лельными плоскостями полусфе­ру АВС и цилиндр A'B'C'D' (рис. 6) с основанием того же радиуса R, что и шар, и с высо­той, равной радиусу, с входящим в него конусом C'D'O', который имеет своим основанием верхнее основание цилиндра, а верши­ной — центр нижнего основания.

На основании принципа Кавальери мы вправе сделать за­ключение, что объем шара равен объему тела, получаемого вырезыванием конуса из цилиндра. В самом деле, легко видеть, что круг ab, полученный в сечении сферы плоскостью , равновелик с кольцом a'c'd'b', получаемым в сечении вышеуказанного тела той же самой плоскостью. Действительно, на основании теоремы Пифагора в полусфере