Реферат: Шар и сфера
площадь одной из боковых граней
![]() ;
;
полная площадь поверхности пирамиды
![]() .
.
Высота пирамиды MM0, как катет треугольника MM0K, равна
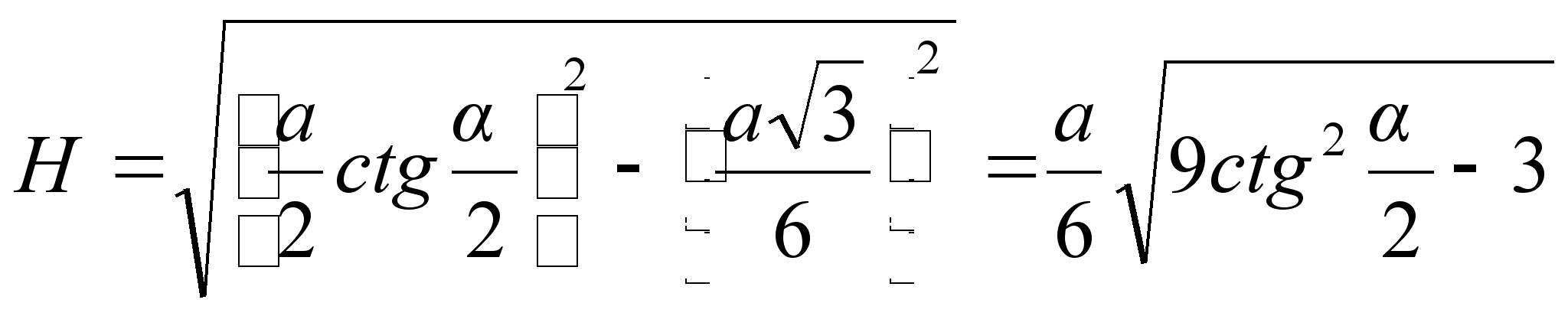 .
.
Объём пирамиды
![]() .
.
Для радиуса вписанного шара находим
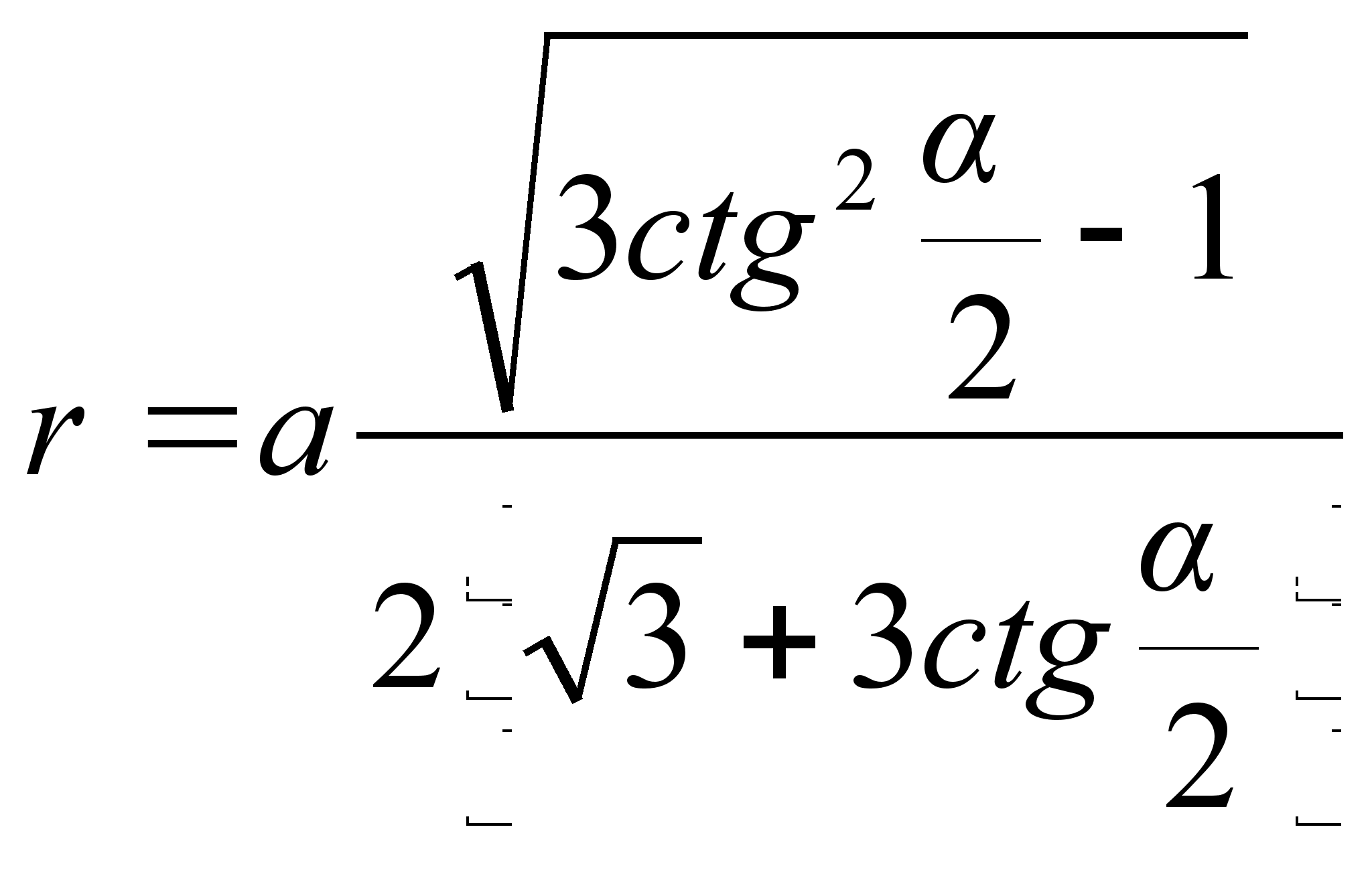 ;
; ![]() .
.
Ответ: ![]() .
.
2.10. Площадь поверхности шара.
З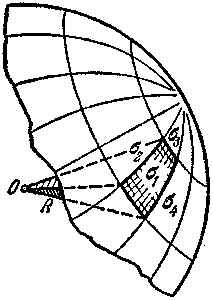 десь даётся очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 17) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не п
десь даётся очень простой, хотя и не совсем строгий вывод формулы для площади сферической поверхности; по своей идее он очень близок к методам интегрального исчисления. Итак, пусть дан некоторый шар радиуса R. Выделим на его поверхности какую-либо малую область (рис. 17) и рассмотрим пирамиду или конус с вершиной в центре шара О, имеющие эту область своим основанием; строго говоря, мы лишь условно говорим о конусе или пирамиде, так как основание не п![]() лоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, на пример, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере). Тогда, обозначая через
лоское, а сферическое. Но при малых размерах основания по сравнению с радиусом шара оно будет весьма мало отличаться от плоского (так, на пример, при измерении не очень большого земельного участка пренебрегают тем, что он лежит не на плоскости, а на сфере). Тогда, обозначая через ![]() площадь этого участка—основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):
площадь этого участка—основание «пирамиды», найдем ее объем как произведение одной трети высоты на площадь основания (высотой служит радиус шара):
![]() . (2.10.1)
. (2.10.1)
Если теперь всю поверхность шара разложить на очень большое число N таких малых областей ![]() , тем самым объем шара—на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой
, тем самым объем шара—на N объемов «пирамид», имеющих эти области своими основаниями, то весь объем представится суммой
![]() , (2.10.2)
, (2.10.2)
где последняя сумма равна полной поверхности шара:
![]() . (2.10.3)
. (2.10.3)
Итак, объем шара равен одной трети произведения его радиуса на площадь поверхности. Отсюда для площади поверхности имеем формулу
![]() , (1.10.4) или
, (1.10.4) или ![]() . (2.10.5)
. (2.10.5)
Последний результат формулируется так:
Площадь поверхности шара равна учетверенной площади его большого круга.
2.11. Площадь поверхности сектора шара.
Приведенный вывод пригоден и для площади поверхности сектора шара (имеем в виду только основание, т. е. Сферическую поверхность, или «шапочки»; см. рис. 14). И в этом случае объем сектора равен одной трети произведения радиуса шара на площадь его сферического основания:
![]() , (2.11.1)
, (2.11.1)
откуда находим для площади шапочки формулу
![]() . (2.11.2)
. (2.11.2)
2.12. Площадь поверхности шарового пояса.
Шаровым поясом (см. рис. 13) называют сферическую поверхность шарового слоя. Чтобы вычислить площадь поверхности шарового пояса, находим разность поверхностей двух сферических шапочек: