Математика / Реферат: Шпора 2

Реферат: Шпора 2

Вопрос №2

Теорема: Пусть z = f(x,y) – ограниченная функция, заданная на прямоугольнике R = [a,b;c,d], и существует двойной интеграл по этому прямоугольнику

Если для " X [a,b] существует одномерный интеграл

то $ повторный интеграл

Доказательство:

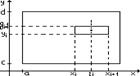
Разобьем отрезки ab и cd отрезками a=x0 <x1 <…<xn =b, c=y0 <y1 <…<yn =d. Рассмотрим теперь частичный прямоугольник Rik =[xi ,xi+1 ;yi ,yi+1 ] mik =inf f(x,y) Mik =sup f(x,y)

Rik Rik

На промежутке [xi ;xi +1 ] возьмём точку x. Будем рас- сматривать точки, лежащие на прямой x = x.

Получаем следующее неравенство mik £ f(x;y)£ Mik yk £ y£ yk +1 Проинтегрируем его по отрезку [yk ; yk +1 ]

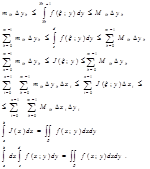
Замечание: если же существует двойной интеграл и существует одномерный интеграл

то существует повторный

Если же функция f(x;y) такова, что существует двойной интеграл по области R, существуют оба од- номерных J(y) и Ί(x), то одновременно имеют место формулы (1) и (2)

Например: если f(x;y) непрерывна в области R, то, как известно двойной интеграл, и оба одномерных существуют, а значит, справедлива формула (3) и для вычисления двойного интеграла можно пользоваться одной из формул (1) или (2), а именно выбирая ту или иную, которая даёт более простое решение.

7.Независемость криволинейного интегр. от пути интегрирования. Теор.1 и 2.

Теорема 1 . Пусть D – ограниченная одно-связанная область плоскости XOY тогда что бы криволинейный интеграл - был равен 0 по любой замкнутой простой кривой , где P(x,y) и Q(x,y) - непрерывны и имеют непрерывные частные производные , необходимо и достаточно что бы во всех точках области D было (2).

Док-во

достаточность : Пусть во всех точках обл. D выполнено рав-во (2) и пусть Г произвольная простая замкнутая кривая, принадлежащая области. Обозначим через D область кот-ю ограничивает эта кривая Г. Применим теперь к этой области ф-лу Грина.

Необходимость : Криволинейный интеграл в любой замкнутой простой кривой существует область D=0. Покажем, что во всех точках области D выполняется рав-во (2). (это доказуется методом от противного). Пусть интеграл = нулю, а рав-во (2) не выполняется, по крайней мере, в одной точке , т.е. . Пусть, так что разность . Пусть тогда . Т.к. частные производные и непрерывны в области D, то непрерывна в этой области, а из непрерывности функций вытекает что ф-ция , то существует окрестность этой точки, принадлежащая области D, так что везде в этой окрестности для любой точки лежащей внутри кривой.

кот-я является границей нашей окрестности - множество чисел внутри . Применим к ф-лу Грина: . Полученное противоречие показывает, что не существует не одной точки где бы равенство (2) не выполнялось.

Теорема 2 Пусть D есть односвязная область плоскости XOY в этой области заданы две непрерывные функции D(x,y) и Q(x,y) имеющие непрерывные частные производные и ; чтоб криволинейный интеграл не зависел от пути интегрирования . Необходимо и достаточно чтоб выполнялось равенство (2).

Док . Не обход. Пусть криволинейный интеграл не зависит от пути интегрирования, а зависит от начальной и конечной точки пути интегрирования.

Возьмём в области D произвольно простую замкнутую кривую Г. На этой кривой т. А и т. В

Т.к. по условию криво-ный интеграл не зависит от пути интегрирования, то интеграл по кривым АmB=AnB

В силу 1-й теоремы должно выполнятся рав-во (2).

Док . Достат. Пусть выполняется рав-во (2) . Покажем, что криволенейный интеграл не зависит от пути интегрирования :

1-й случай . Берём две произвольные точки принадлежащие области D и соединяем эти точки непрерывными кривыми и , кот-е не имеют точек самопересечения.

Если эти кривые образуют простой замкнутый контур без самопересечения и т.к. выполняется рав-во (2), то интеграл поэтому замкнутому контуру обязан быть равен 0. , т.е. интеграл не зависит от кривой.

2-й случай . Пусть и имеют конечное число точек самопересечения

Будем двигаться от А к C1 в результате получили контур и . Аналогично Для всех остальных случаев.

К-во Просмотров: 1160
Бесплатно скачать Реферат: Шпора 2