Реферат: Случайные вектора
50.2. Рассмотрим геометрическую интерпретацию функции ![]() . Пусть случайные величины
. Пусть случайные величины ![]() ,
, ![]() являются компонентами случайного вектора
являются компонентами случайного вектора ![]() . Тогда результат каждого опыта по измерению случайного вектора
. Тогда результат каждого опыта по измерению случайного вектора ![]() можно рассматривать как точку на плоскости, а функция
можно рассматривать как точку на плоскости, а функция ![]() определяет вероятность попадания точки в часть плоскости:
определяет вероятность попадания точки в часть плоскости: ![]() , выделенной на рис. 50.1 штриховкой.
, выделенной на рис. 50.1 штриховкой.

Рис. 50.1. Геометрическая интерпретация функции ![]() .
.
Представим вероятность ![]() - попадания случайного вектора
- попадания случайного вектора ![]() в прямоугольник
в прямоугольник ![]() ,
, ![]() ,
, ![]() ,
, ![]() , рис 50.2, через функцию
, рис 50.2, через функцию ![]() . Несложно определить, что
. Несложно определить, что

Рис. 50.2. К вычислению вероятности попадания в прямоугольник.
![]()
(50.2)
Пусть ![]() ,
, ![]() - малые величины и функция
- малые величины и функция ![]() имеет первые производные по
имеет первые производные по ![]() и
и ![]() , а также вторую смешанную производную, тогда из (50.2) следует:
, а также вторую смешанную производную, тогда из (50.2) следует:

 . (50.3)
. (50.3)
Отсюда:
 . (50.4)
. (50.4)
Совместная плотность распределения вероятности двух случайных величин
Пусть у функции ![]() существуют производные по
существуют производные по ![]() ,
, ![]() , а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин
, а также вторая смешанная производная. Совместной (или двумерной) плотностью распределения вероятностей случайных величин ![]() и
и ![]() называется функция
называется функция
 (51.1)
(51.1)
Рассмотрим основные свойства двумерной плотности вероятности.
1. Справедливо соотношение:
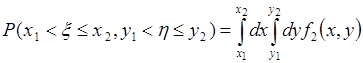 . (51.2)
. (51.2)
Для доказательства используем равенство (51.1), тогда:
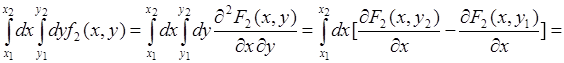
![]() . (51.3)
. (51.3)
Теперь из равенства (50.2) следует (51.2). Это соотношение имеет практическое значение, поскольку позволяет вычислять вероятность ![]() - попадания двумерного вектора
- попадания двумерного вектора ![]() в прямоугольник, определяемый отрезками
в прямоугольник, определяемый отрезками ![]() и
и ![]() через плотность вероятности
через плотность вероятности ![]() .
.
2. Рассмотрим частный случай соотношения (51.2). Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда (51.2) принимает вид:
, тогда (51.2) принимает вид:
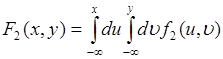 . (51.4)
. (51.4)
Это соотношение определяет функцию распределения вероятностей ![]() через плотность вероятности
через плотность вероятности ![]() и является обратным по отношению к равенству (51.1).
и является обратным по отношению к равенству (51.1).
3. Рассмотрим (51.2) при условиях: ![]() ,
, ![]() ,
, ![]() ,
, ![]() , тогда из (51.2) следует равенство:
, тогда из (51.2) следует равенство:
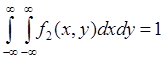 , (51.5)
, (51.5)
поскольку ![]() - как вероятность достоверного события. Соотношение (51.5) называется условием нормировки для плотности вероятности
- как вероятность достоверного события. Соотношение (51.5) называется условием нормировки для плотности вероятности ![]() .
.
4. Если ![]() - плотность вероятности вектора
- плотность вероятности вектора ![]() , и
, и ![]() - плотность вероятности случайной величины
- плотность вероятности случайной величины ![]() , то
, то