Реферат: Случайные вектора
где ![]() и
и ![]() . При этом
. При этом ![]() выражается через индивидуальные характеристики
выражается через индивидуальные характеристики ![]() и
и ![]() , т.е. каких-либо групповых эффектов в
, т.е. каких-либо групповых эффектов в ![]() не проявляется, что является следствием независимости случайных величин
не проявляется, что является следствием независимости случайных величин ![]() и
и ![]() . Из цепочки преобразований (54.4) следует равенство
. Из цепочки преобразований (54.4) следует равенство ![]() - математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
- математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.
54.2. Аналогично (54.2) числа
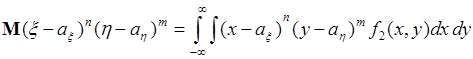 (54.5)
(54.5)
называются центральными смешанными моментами, порядка ![]() . Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
. Наиболее важной групповой характеристикой двух случайных величин среди чисел (54.5) является ковариация
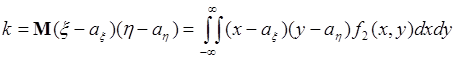 , (54.6)
, (54.6)
которая является центральным смешанным моментом порядка ![]() . Для ковариации используется также обозначение:
. Для ковариации используется также обозначение: ![]() . Если
. Если ![]() , то
, то ![]() - совпадает с дисперсией случайной величины
- совпадает с дисперсией случайной величины ![]() .
.
Если ![]() и
и ![]() - независимы, то из (54.6) следует, что ковариация
- независимы, то из (54.6) следует, что ковариация
![]() .
.
Обратное утверждение в общем случае неверно, т.е. из равенства ![]() в общем не следует независимость случайных величин
в общем не следует независимость случайных величин ![]() и
и ![]() . В частности, обратное утверждение справедливо, если
. В частности, обратное утверждение справедливо, если ![]() и
и ![]() - гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
- гауссовы случайные величины. Более подробно этот вопрос обсуждается ниже.
54.3. Найдем связь между корреляцией ![]() и ковариацией
и ковариацией ![]() случайных величин
случайных величин ![]() и
и ![]() . Из определения ковариации (54.6) следует
. Из определения ковариации (54.6) следует
![]()
![]() .
.
Таким образом, ковариация ![]() и корреляция
и корреляция ![]() связаны соотношением
связаны соотношением
![]() . (54.7)
. (54.7)
Верхняя и нижняя границы корреляции и ковариации
55.1. Пусть случайные величины ![]() и
и ![]() имеют математические ожидания
имеют математические ожидания ![]() ,
, ![]() , дисперсии
, дисперсии ![]() ,
, ![]() , корреляцию
, корреляцию ![]() и ковариацию
и ковариацию ![]() . Рассмотрим неравенство
. Рассмотрим неравенство
 . (55.1)
. (55.1)
Возведем в квадрат, затем оператором математического ожидания подействуем на каждое слагаемое, тогда (55.1) принимает вид:
 ,
,
что далее сводится к неравенству
![]() . (55.2)
. (55.2)
Его левая часть ![]() может быть как положительной так и отрицательной, правая часть - только положительна. Поэтому неравенство (55.2) обычно записывается в более сильном варианте:
может быть как положительной так и отрицательной, правая часть - только положительна. Поэтому неравенство (55.2) обычно записывается в более сильном варианте:
![]() . (55.3)
. (55.3)
Таким образом, корреляция ![]() случайных величин
случайных величин ![]() и
и ![]() принимает значения из интервала
принимает значения из интервала ![]() .
.
Соотношение, аналогичное (55.3) можно получить и для ковариации ![]() , если в исходном выражении (55.1) вместо
, если в исходном выражении (55.1) вместо ![]() подставить центрированную случайную величину
подставить центрированную случайную величину ![]() и вместо
и вместо ![]() соответственно
соответственно ![]() . При этом необязательно выполнять все преобразования, аналогичные (55.1) - (55.3), достаточно учесть, что замена
. При этом необязательно выполнять все преобразования, аналогичные (55.1) - (55.3), достаточно учесть, что замена ![]() и
и ![]() приводит к замене
приводит к замене ![]() на
на ![]() ,
, ![]() на
на ![]() , а также
, а также ![]() на
на ![]() . Поэтому из (55.3) следует
. Поэтому из (55.3) следует
![]() . (55.4)
. (55.4)
55.2. Неравенства, определяющие область значений корреляции ![]() и ковариации
и ковариации ![]() , аналогичные (55.3), (55.4), можно получить в другом виде на основе следующего очевидного неравенства:
, аналогичные (55.3), (55.4), можно получить в другом виде на основе следующего очевидного неравенства:
![]() . (55.5)
. (55.5)
Отсюда ![]() , поэтому справедливо неравенство
, поэтому справедливо неравенство
 . (55.6)
. (55.6)