Реферат: Случайные вектора

. (55.7)

Ковариация и независимость двух случайных величин

Для независимых случайных величин и ковариация . В отличие от этого рассмотрим другой крайний случай, когда случайные величины и связаны функциональной зависимостью:

, (56.1)

где - числа. Вычислим ковариацию случайных величин и :

. (56.2)

Из (56.1) следует . Подставим этот результат в (56.2), тогда

. (56.3)

Из (56.1) определим дисперсию

, (56.4)

откуда . Это равенство подставим в (56.3), тогда

(56.5)

Таким образом, ковариация линейно связанных случайных величин и принимает максимальное значение , если , или минимальное значение , если , на отрезке допустимых значений для в общем случае (согласно формуле (55.4)).

В связи с этим можно выдвинуть предположение о том, что ковариация является мерой статистической связи между случайными величинами и . Действительно, для двух крайних случаев получены подходящие для этого результаты, а именно: для независимых величин , а для линейно связанных максимален. Далее будет показано, что это предположение верно, но не в общем, а только для статистической связи линейного типа. Эта связь характерна тем, что при усилении этой связи растет , и в пределе связь вырождается в линейную зависимость (56.1).

Однако если связь имеет нелинейный характер, то величина не отражает меру (степень) этой связи. Рассмотрим следующий пример. Пусть , , и - случайная величина с равномерным на интервале распределением вероятностей. Случайные величины и связаны между собой соотношением: . Таким образом, между величинами и существует функциональная связь, а не статистическая, и следовало ожидать, что величина максимальна. Однако, прямые вычисления приводят к результату . Действительно,

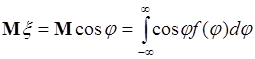, (56.6)

где

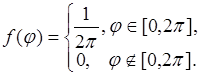
- плотность распределения вероятностей случайной величины . С учетом этого (56.6) преобразуется:

.

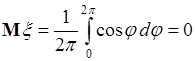Аналогично

,

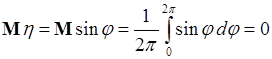теперь ковариация

.

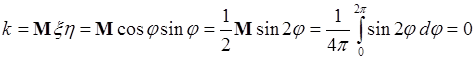Таким образом, для нелинейной связи между случайными величинами их ковариация не может использоваться как мера статистической связи, поскольку значение ковариации не отражает степень этой связи.

Ковариация и геометрия линий равного уровня плотности вероятности

Ковариация случайных величин и определяется через их совместную плотность вероятности соотношением:

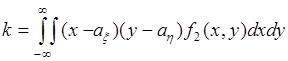. (57.1)

Подынтегральная функция в (57.1) неотрицательна для таких , , при которых , то есть при , или , . И наоборот, при , или , подынтегральная функция (57.1) отрицательна либо равна нулю. Знак ковариации зависит от того, какие значения, положительные или отрицательные преобладают в подынтегральной функции. Поэтому знак числа определяется расположением линий равного уровня плотности вероятности . На рис. 57.1 представлен пример линий равного уровня функции , для которой . Штриховкой

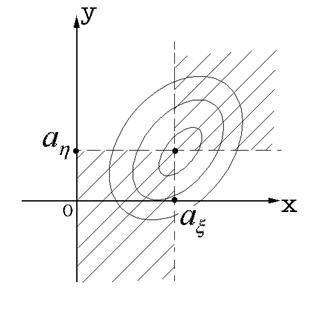
Рис. 57.1.