Реферат: Техническая эксплуатация автомобилей. Расчет вероятности безотказной работы деталей ЦПГ
_
f э (l i ) = ni / (N * Dl ) ,
г) рассчитаем нормированные и центрированные отклонения середины интервалов:
__ _ _
yi = (l i - a) / s ,
д)определим значения теоретической плотностираспределения вероятностей f т (l i ) по формуле: _ _
f т (l i ) = (1 / s) * f о (yi ), где
___
f о (yi ) = (1 / Ö2p) * exp( -yi 2 / 2)
Полученные значения расчетов в пунктах в, г, д сведем в таблицу 4.
ТАБЛИЦА 4.
Таблица вычислений эмпирической и теоретической плотности распределения вероятностей и нормированных и центрированных отклонений середины интервалов.
| n i \ Параметры | y i | f э (l i ) | f о (l i ) | f т (l i ) |
| n1 | -2,262 | 0,0013 | 0,0333 | 0,0007 |
| n2 | -1,485 | 0,0025 | 0,1333 | 0,0029 |
| n3 | -0,707 | 0,0063 | 0,3278 | 0,0071 |
| n4 | 0,071 | 0,0072 | 0,4 | 0,0086 |
| n5 | 0,848 | 0,0088 | 0,2857 | 0,0062 |
| n6 | 1,626 | 0,0013 | 0,1089 | 0,0023 |
| n7 | 2,404 | 0,0004 | 0,0222 | 0,0005 |
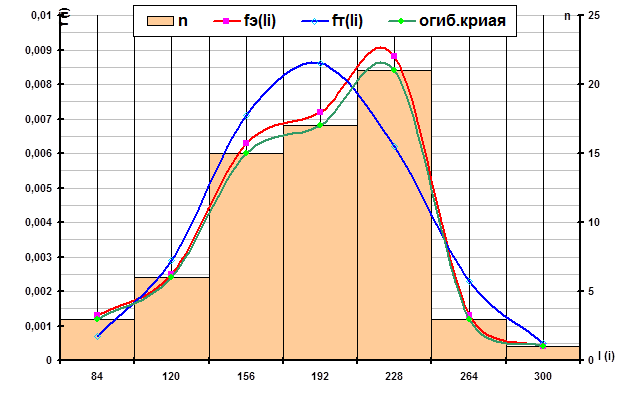 |
?) ?? ??????????? ???????? ?????? ?? ??????? 1 ???????????: ???????????? ??????, ????????????? ?????????? ???????????? f э (l i ) , ????????????? ?????? ????????????? f т ( l i ) ? ????????????? ??????.
Рис.1. Гистограмма середины интервалов, кривая распределения плотностей вероятностей f э (l i ) , теоретическую кривую распределения f т ( l i ) и выравнивающая(огибающая) кривая.
п.3.1.5. Проверка согласия между эмпирическим и теоретическим (нормальным) законом распределения по критерию c2 Пирсона :
а.) Определим меру расхождения c2 между эмпирическим и теоретическим распределениями:
r
c2 = S (ni - ni `)2 / ni ` , где
i=1
ni и ni ` -- соответствие эмпирической и теоретической частоты попадания случайной величины в i-ый интервал.
Для удобства вычислений критерий c2 определим по формуле:
r _ _ _
c2 = N * Dl * S [ fэ (l i ) - fт (l i ) ]2 / fт (l i ) ,
i=1
c 2 =5,12
б.) Вычислим число степеней свободы m ( при этом интервалы, в которых частоты ni меньше 5-ти объединим с соседними интервалами):
m = r1 - k - 1, где
r1 -- число интервалов полученное при объединении;
k – количество параметров закона распределения.
Нормальный закон является двухпараметрическим и определяется математическим ожиданием и средним квадратичным отклонением , т.е. k =2.
m = 4-2-1 = 1