Реферат: Теоретические основы и методы системного анализа оптимизации управления принятия решений и

Метрика должна удовлетворять некоторым определяющим свойствам:

а) r ≥ 0 при любых а,b,c;

б) r(a,b) = 0 тогда и только тогда, когда a = b (аксиома идентичности);

в) r(a,b) = r(b,a) (аксиома симметричности);

г) r(a,b) £r(а,с) + r(с,b) (аксиома треугольника).

Пара (Х,r_Х ) называется метрическим пространством.

Примеры метрик:

а) r(а,b) = |a - b|;

б) r₂ (a,b) = -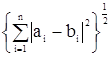

евклидова метрика в евклидовом пространстве Rⁿ ,

в) r_¥ (а,b) =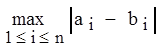- чебышевская метрика;

г) r_К (a,b) = 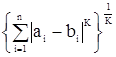- метрика Гельдера, К – целое.

В общем случае – отношения бывают: унарные (самого с собой); бинарные (между двумя элементами); тернарные (между тремя элементами); вообще, - n-арные.

4) Организация

Введем в рассмотрение понятие «состояние» элемента или системы. Количество состояний (мощность множества состояний) может быть конечно, счетно (количество состояний измеряется дискретно, но их число бесконечно); мощности континуум (состояния изменяются непрерывно и число их бесконечно и несчетно).

Состояния можно описать через переменные состояния . Если переменные – дискретные, то количество состояний может быть либо конечным, либо счетным. Если переменные – аналоговые (непрерывные), тогда - мощности континуум.

Минимальное количество переменных, через которые может быть задано состояние, называется фазовым пространством . Изменение состояния системы отображается в фазовом пространстве фазовой траекторией .

Уравнение состояния системы:

Y = F(X, Z), (1.1)

где Z – переменные состояния (вектор аналоговых или дискретных величин),

Х – входные переменные, Y – выходные переменные системы.

Одной из наиболее часто используемых характеристик организации является энтропия (поворот, превращение – греч.).

Энтропия систем

Степень организации элементов в системе связывается с изменением (снижением) энтропии системы по сравнению с суммарной энтропией элементов. Понятие энтропии введено Больцманом для термодинамических систем:

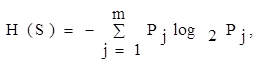(1.2)

где - вероятность j-го состояния (в теории информации – события); m - возможное число состояний (событий).

Например, два элемента А и В могут каждый принимать два равновероятных состояния: «0»и «1». Вероятность каждого состояния:

Р₁ (А) = Р₂ (А) = Р₁ (В) = Р₂ (В) = 0,5.

Для одного элемента энтропия составит