Реферат: Теоретические основы и методы системного анализа оптимизации управления принятия решений и

Энтропия двух элементов:

Н(А) + Н(В) = 1 + 1 = 2.

¨ Допустим, что система S элементов А и В может принимать три состояния: «-1», «0», «1» с вероятностями Р₁ (S) = Р₃ (S) = 0,2; Р₂ = 0,6.

Тогда

Н(S) = -2^. 0,2^. log₂ 0,2 - 0,6^. log₂ 0,6 = -0,4×(-2,32) - 0,6×(-0,737) = 1,37.

Энтропия системы S меньше суммы энтропий элементов А и В на

DН = Н(А) + Н(В) - Н(S) = 2 - 1,37 = 0,63.

¨ Для расчета изменения энтропии системы через вероятности состояний очень часто используется метод Колмогорова . Допустим, дана структурная схема (граф) состояний подсистемы S. Исходным состоянием системы с равной степенью вероятности может быть одно из четырех состояний, т.е. . Будем считать, что интенсивности переходов l₂₁ , l₃₂ , l₄₃ , l₁₄ , l₂₄ заданы. Тогда можно показать, что скорости изменения вероятности нахождения системы в i-м состоянии определяются как

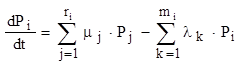, (1.3)

где ; n – число узлов графа (количество состояний);

m_j - интенсивности переходов по дугам, входящим в i-й узел;

r_i – число дуг, входящих в i-й узел;

l_k - интенсивности переходов по дугам, исходящим из i-го узла;

m_i – число дуг, выходящих из i-го узла;

P_i и P_j – вероятности нахождения системы в i-м и j-м состояниях соответственно.

Заметим, что

.

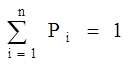Установившееся значение вероятности нахождения системы в i-м состоянии определяется из условия

.

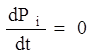Тогда для системы с n состояниями имеем систему из (n + 1) уравнений с n неизвестными:

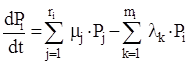;. (1.4)

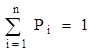
Одно из уравнений (1.4) можно отбросить, так как оно может быть получено из (n - 1) оставшихся.

Пример. Примем l₂₁ = 0,1, l₃₂ = 0,2, l₄₃ = 0,3, l₁₄ = 0,4, l₂₄ = 0,5. Тогда получаем:

l₁₄ ^. Р₄ - l₂₁ ^. Р₁ = 0

l₂₁ ^. Р₁ + l₂₄ ^. Р₄ - l₃₂ ^. Р₂ = 0

l₃₂ ^. Р₂ - l₄₃ ^. Р₃ = 0

l₄₃ ^. Р₃ – (l₁₄ + l₂₄ )^. Р₄ = 0

Р₁ + Р₂ + Р₃ + Р₄ = 1.