Реферат: Теоретические основы и методы системного анализа оптимизации управления принятия решений и

- 0,1^. Р₁ + 0^. Р₂ + 0^. Р₃ + 0^. Р₄ = 0

0^. Р₁ + 0,2^. Р₂ – 0,3^. Р₃ + 0^. Р₄ = 0

0^. Р₁ + 0^. Р₂ + 0,3^. Р₃ – 0,9^. Р₄ = 0

1^. Р₁ + 1^. Р₂ + 1^. Р₃ + 1^. Р₄ = 1.

Решение полученной системы: Р₁ = 0,32, Р₂ = 0,36, Р₃ = 0,24, Р₄ = 0,08.

Расчет энтропий ведется по формуле

.

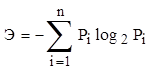Для исходного состояния

Э₀ = -4 ^. 0,25 ^. log₂ 0,25 = 2,

Для конечного состояния

Э_к = - (0,32 ^. log₂ 0,32 + 0,36 ^. log₂ 0,36 + 0,24 ^. log₂ 0,24 + 0,08 ^. log₂ 0,08) = 1,835.

То есть, изменение энтропии составляет

DЭ = Э₀ – Э_к = 2 – 1,835 = 0,165.

Существуют два основных подхода к расчету энтропий систем и ценности информации.

Первый подход основан на декомпозиции исходной задачи на этапы вычисления вероятностей апостериорной и априорной вероятности элементарных событий.

Методика расчета включает:

· декомпозицию исходной задачи на последовательность таких элементарных событий, априорная вероятность которых известна, а апостериорная может быть легко рассчитана;

· расчет энтропий (или ценности информации) каждого элементарного события;

· вычисление изменения энтропии исходного состояния по отношению к конечному (или ценности информации) путем суммирования изменений энтропий элементарных этапов (переходов, событий).

Данный подход позволяет избежать вычисление вероятности сложных событий.

Второй подход основывается на использовании условных вероятностей событий. Последние иногда рассчитать довольно сложно.

Таким образом, энтропия выступает в качестве меры хаоса, беспорядка и ее снижение означает увеличение организации.

Для информационных систем степень организации очень часто зависит от количества информации, которая может быть использована для управления.

1.2 Количество информации

В теории информации количество информации часто измеряют в битах (binarydigital), где бит, определяется как ценность I информации об исходе двух равновероятных событий. Например, эта информация о том, что сейчас день, а не ночь.

Вероятность каждого из событий

Р(Д) = 0,5; Р(Н) = 0,5;

I = log₂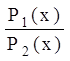 , (1.5)

где Р₁ (х) – апостериорная вероятность; Р₂ (х) – априорная вероятность.