Реферат: Теория игр, рафический метод в теории игр

Основной целью теории игр является выявление для каждого из игроков «оптимальных стратегий».

Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку максимально возможный средний выигрыш (или, эквивалентно, минимально возможный средний проигрыш).Выбор оптимальной стратегии базируется на принципе, предполагающем, что обаигрока разумны в одинаковой степени и поведение каждого из них направлено напротиводействие противнику в достижении его цели. Таким образом, теория играбстрагируется от ошибок, просчетов, азарта и риска, присущих игрокам, реальных конфликтах.

Будем считать, что выигрыш одного игрока равен в точности проигрышу

второго игрока, такая игра называется игрой с нулевой суммой . Конечная игра двух игроков с ненулевой суммой, в которой выигрыши каждого игрока задаются матрицами отдельно для соответствующего игрока, называется биматричной игрой .

2.Матричные игры

Матричной игрой называется конечная игра двух игроков с нулевой

суммой, в которой задается выигрыш игрока 1 в виде матрицы, строка матрицы

соответствует номеру применяемой стратегии игрока 1, столбец – номеру применяемой стратегии игрока 2; на пересечении строки и столбца матрицы

находится выигрыш игрока 1, соответствующий применяемым стратегиям.

Пусть играют 2 игрока P1 и P2. Матрица

элементы aij – выигрыш игрока P1, если P1 – выбирает i строку, а P2 – выбирает j столбец, называется платежной матрицей игры .

Пусть игрок P1 выбирает i строку с вероятностью xi , P2 выбирает j столбец с

вероятностью yj , тогда и будут называться соответственно смешанными стратегиями 1-ого и 2-ого игроков .

Замечание : так как компонентами смешанных стратегий X и Y являются

вероятности, то и . Если среди компонентов смешанной стратегии X только одна 1, остальные 0, то стратегия называется чистой .

- i -ая чистая стратегия. Любую смешанную стратегию можно представить в виде выпуклой комбинации чистых стратегий, т.е.

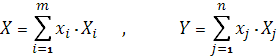
Пример . Представить смешанную стратегию в виде выпуклой

комбинации чистых стратегий.

Решение.

Платежной функцией (X ,Y ) первого игрока называется математическое

ожидание его выигрыша, т.е.

(X ,Y )=

Решением матричной игры называют пару смешанных стратегий и

число v называемое ценой игры, удовлетворяющих следующим условиям:

1)

Если P1 придерживается своей оптимальной стратегии X *, то какую бы

чистую стратегию не принимал второй игрок P2, P1 получит выигрыш не меньше чем цена игры v .

2)