Реферат: Теория игр, рафический метод в теории игр
Платежная функция

Решить игру с платежной матрицей

Положим ![]() . Тогда
. Тогда
![]()
![]() . Тогда
. Тогда
 Если
Если ![]() - оптимальная стратегия первого игрока, то по определению
- оптимальная стратегия первого игрока, то по определению
решения матричной игры
 Если игра с нулевой суммой, то (
Если игра с нулевой суммой, то (![]() -цена игры).
-цена игры).
Решая систему, получим ![]() .
.

Аналогично для второго игрока:

![]() Тогда
Тогда
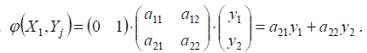
![]() Тогда
Тогда
Если ![]() - оптимальная стратегия второго игрока.
- оптимальная стратегия второго игрока.
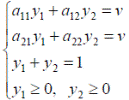 Если игра с нулевой суммой, то (
Если игра с нулевой суммой, то (![]() -цена игры).
-цена игры).
Решая систему, получим ![]() .
.
Пример. Найти решение игры заданной платежной матрицей A= ![]() .
.
Решение:
Решим игру. Пусть ![]() - оптимальная стратегия первого игрока,
- оптимальная стратегия первого игрока, ![]() - оптимальная стратегия второго игрока,
- оптимальная стратегия второго игрока,![]() -цена игры. Тогда оптимальные стратегии игроков и цену игры можно найти, решив системы:
-цена игры. Тогда оптимальные стратегии игроков и цену игры можно найти, решив системы:
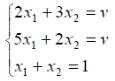
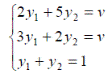
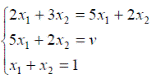
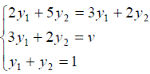
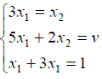
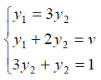
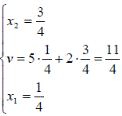
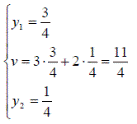
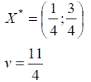
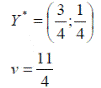
Ответ: оптимальные стратегии игроков ![]() , цена игры
, цена игры ![]() .
.