Реферат: Теория игр, рафический метод в теории игр

Алгоритм:

1) Через концы горизонтального отрезка [0;1] провести два перпендикуляра к нему: левый и правый. Каждой точке отрезка [0;1] будем ставить некоторую смешанную стратегию (x;1− x).

2) На левом перпендикуляре от точки 0 отложить элементы . На правом перпендикуляре от точки 1 отложить элементы .

Замечание. Масштабы на левом и правом перпендикулярах должны быть

одинаковы, не обязательно совпадающие с масштабом горизонтального отрезка [0;1].

3) Соединить отрезками элементы .

4) Выделить нижнюю огибающую всех построенных отрезков, и найти максимальную точку (точки). Пусть точка является пересечением отрезков и . Тогда оптимальную стратегию можно найти при помощи матрицы .

Решить игру с платежной матрицей A= графически.

Решение:

1. Через концы горизонтального отрезка [0;1] проведем 2 перпендикуляра к нему. Каждой точке отрезка [0;1] будем ставить смешанную стратегию (x ; 1− x ).

2. На левом перпендикуляре от точки 0 отложить элементы 2, 3, 11. На правом перпендикуляре от точки 1 отложить элементы 7, 5, 2.

3. Соединить отрезками элементы 2 и 7, 3 и 5, 11 и 2.

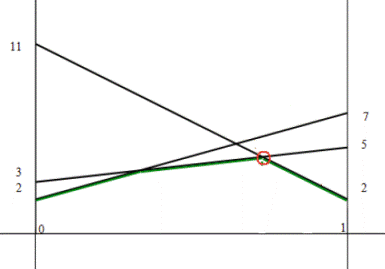
4. Выделим нижнюю огибающую всех построенных отрезков, и найдем

максимальную точку. Точка является пересечением отрезков [3;5] и [11;2]. Тогда оптимальную стратегию можно найти при помощи матрицы .

Решим игру с платежной матрицей .

Оптимальные стратегии игроков и цену игры можно найти, решив системы:

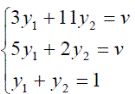
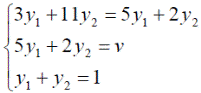
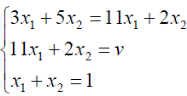
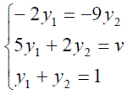
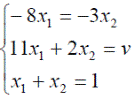
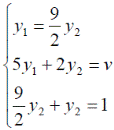
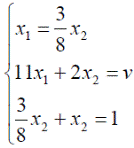
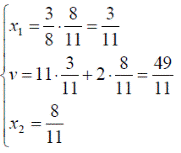
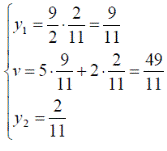
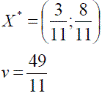
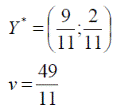
Ответ: оптимальные стратегии игроков оптимальные стратегии игроков 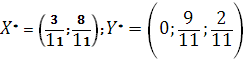, цена игры

2.Решение игр с платежной матрицей m ×2

Решить игру с платежной матрицей A=.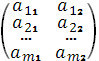

Алгоритм :

1) Через концы горизонтального отрезка [0;1] провести два перпендикуляра к нему: левый и правый. Каждой точке отрезка [0;1] будем ставить некоторую смешанную стратегию (y;1− y).

2) На левом перпендикуляре от точки 0 отложить элементы . На правом перпендикуляре от точки 1 отложить элементы .

3) Соединить отрезками элементы .