Следовательно, структурная группа звеньев 2-3 является структурной группой 2 класса (число подвижных звеньев n=2), 2 порядка (структурная группа имеет 2 поводка), 1 вида (ВВВ).

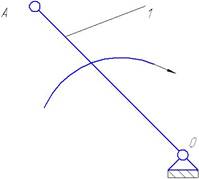
Рисунок 4

Группа звеньев 0 – 1 (рисунок 4). Данная группа состоит из подвижного звена кривошипа 1, стойки 0 и одной кинематической пары:

0 – 1 – вращательная пара пятого класса;

тогда и .

Подставляя найденные значения коэффициентов в формулу Чебышева, получим:

Данный результат означает, что для однозначного определения возможных положений звеньев данного механизма достаточно одной обобщенной координаты.

Следовательно, группа звеньев 0 – 1 не является структурной группой Ассура, а представляет собой первичный механизм, подвижность которого равна 1.

Из проведённого анализа следует, что подвижность данного сложного рычажного механизма равна 1; механизм имеет следующий структурный состав: первичный механизм с подвижностью равной 1 и две структурные группы 2 класса, 2 порядка, 1 и 2 вида.

Первичный механизм.

??????????? ??????? ?????????

	+

Вывод:

Из проведенного анализа следует , что подвижность механизма равна 1. Механизм имеет следующий структурный состав: первичный механизм с подвижностью равной 1, и две структурные группы Ассура 2 класса, 2 порядка, 1 и 2 вида. Класс механизма определяется наивысшим классом структурной группы, входящей в его состав, следовательно данный механизм 2 класса.

2 Синтез кинематической схемы плоского рычажного механизма по заданным параметрам

Чтобы построить кинематическую схему плоского рычажного механизма по заданным параметрам, нужно найти масштабный коэффициент длины , который рассчитывается по формуле:

где – действительная длина коромысла в метрах;

– размер коромысла в миллиметрах принимаемый на чертеже.

Остальные размеры звеньев вычислим по формуле:

где i – номер звена, для которого вычисляется длина на кинематической схеме.

Переходим к построению положения звеньев механизма.

Для этого на плоскости выбираем точку . Относительно ее находим расположение точки и линии, вдоль которой движется ползун. Из точки радиусом проводим окружность. Из точки проводим дуги окружностей радиусами и . Проводим отрезок , из точки А -отрезок длиной до пересечения с дугой окружности радиусом . Затем из получившейся точки В строим отрезок ВС = , проходящий через - мы нашли точку С . Из нее проводим прямую длиной до пересечения с линией движения ползуна и в результате этого мы нашли точку D .

3 Кинематический анализ

3.1 Построение 12-ти планов положений

Построим двенадцать положений механизма в масштабном коэффициенте м/мм (лист 1). Чтобы найти крайние положения, надо из точки О провести отрезки длиной (крайнее верхнее положение) до пересечения с дугой окружности радиусом и отрезок длинной (крайнее нижнее положение). Верхнее положение кривошипа вдоль этой прямой и будет начальным положением. Каждое новое положение механизма получим поворотом кривошипа на 30 градусов в сторону вращения и повтором действий, описанных в пункте 1.2.

3.2 Построение планов скоростей относительно 12-ти планов положений для седьмого положения механизма

Проанализируем полученную схему механизма: точка О является неподвижной точкой, следовательно, модуль скорости этой точки равен нулю .

Вектор скорости точки А представляет собой геометрическую сумму вектора скорости точки О и скорости относительного вращательного движения точки А вокруг О :

где – вектор скорости точки А ;

– вектор скорости точки О , взятой за полюс;