Реферат: Типы регулярных регуляторов

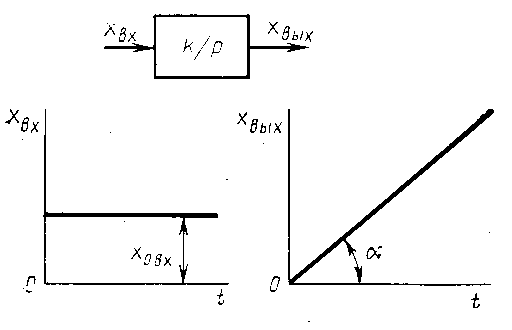
Рисунок 5. Передаточная функция и временная характеристика интегрирующего звена.

На рис.5 Представлен характер изменения выходной величины интегрирующего звена при подаче на его вход постоянной входной величины x _0ВХ , изображение которой x _ВХ ( p )= x _0ВХ / р

Тогда из уравнения W ( p )= 1 / Tp получим

x _0ВХ = L ^-1 [ x _ВЫХ ( p )] = L ^-1 [ k x _0ВХ / p ² ] = k x _0ВХ * t (6)

Таким образом, в этом случае x вых изменяется по прямой, проходящей через начало координат под углом a =arktkx вх оси абсцисс.

Из передаточной функции W ( p )= 1/ Tp звена W ( p )= k / p определяем

W (i w) = k / j w = - j k / w; U (w) = 0;

V (w) = - k / w; W (w) = k / w; j (w) = - p / 2 (7)

Согласно формуле

W ( i w ) = k e ^{– j p / 2} / w . (8)

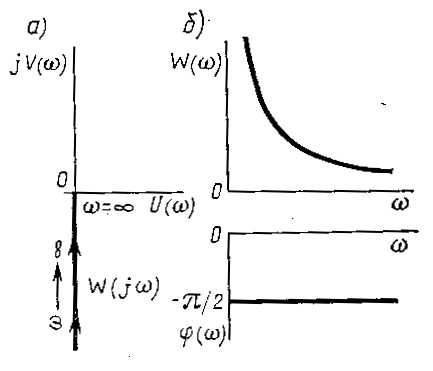
Рисунок 6. Частотные характеристики интегрирующего звена.

Частотные характеристики представлены на рис. 6, из которого следует, что а) КЧХ звенаW ( jw ) при изменение w от 0 до ¥ совпадает с отрицательной мнимой полуосью (рис.6а);

б) при всех частотах выходные колебания отстают по фазе от входных на угол 90° (рис.6в)

в) АЧХ представляет собой гиперболу, т.е. чем меньше частота входного сигнала, тем больше этот сигнал усиливается звеном. При w = 0 коэффициент усиления равен бесконечности, и, наоборот, при w = ¥ коэффициент усиления звена равен нулю (рис.6б).

Логарифмируя W ( w ) в (7), получаем

L (w) = 20 lg k – 20 lg w (9)

Таким образом, ЛАЧХ представляет собой прямую линию, пересекающую при k = 0 ось абсцисс в точке w = 1 и имеющую наклон к оси абсцисс 20 дБ / дек. При k¹ 1 ЛАЧХ перемещается параллельно оси ординат на величину 20 l gk (рис.7а)

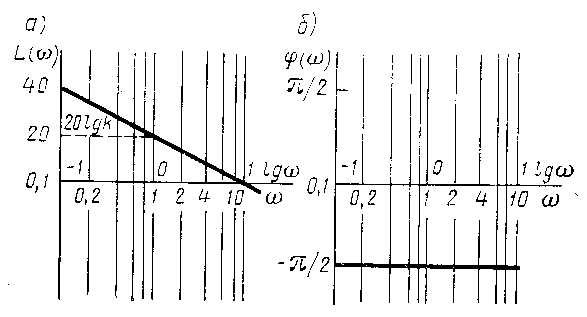
Рисунок 7. Логарифмические частотные характеристики интегрирующего звена.

Логарифмическая фазо-частотная характеристика не зависит от частоты и равна - p / 2 (рис.7б). На рис.7 на оси абсцисс для сравнения указаны значения w и lg w , а также нанесена координатная сетка частот.

Пример1.

Определим динамические свойства гидравлического механизма (рис.8) , который широко применяется в современных системах регулирования. Входной величиной для него является перепад давления p _ВХ = p ₁ - p ₂ , а выходной – перемещение D s _ВЫХ поршня.

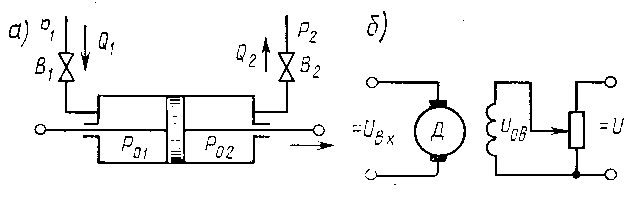
Рисунок 8. Примеры интегрирующих звеньев.

Сила давления на поршень равна p = ( p ₀₁ - p ₀₂ ) F , где F - эффективная площадь поршня. Если пренебречь трением и инерцией поршня. То можно считать, что это усилие целиком расходуется преодоление внешней нагрузки, приложенной к поршню (сопротивление перемещению регулирующего органа, заслонки, шибера и т.п.):

р _{В . Н} = (p₀₁ - p₀₂ ) F (10)

При небольших отклонениях от состояния равновесия расходы жидкости через вентили В1 и В2 пропорциональны перепадам давления на вентилях

Q₁ = k₁ (p₁ - p₀₁ ); Q₂ = k₂ (p₀₂ - p₂ ) (11)